Definition of the definite integrals?
Why is it assumed when calculating the area of the shaded region under the curve y=f(x), above the x-axis and bounded between a pair of vertical lines that the function should be both continuous and defined on the closed interval [a,b], there are many restrictions imposed by the definition.
In the following step function, the function is discontinuous at more than one point yet I can compute the area under each horizontal line because the area of the rectangle is given by (b*h)
Why do we divide the interval into n equal subintervals as the base, when we can still construct a rectangular network, in which each rectangle has a different base. And, we can still find the area of the region if we know how to find the area of each rectangle we can then find the area of the rectangular network.
Area of a whole= Sum of the areas of the parts.
How do we find the area of the shaded region if we take its nature of this region to be an upper edge curve?
If one region is contained within another the area of the contained region is less than or equal than that of the containing region.
In other words
Lower Riemman sum<Area of region<Upper Riemman sum
The nature of the inscribed rectangles is different from that of the region, and that's why I don't quite understand why in the limit these two sums are exactly equal to the area below the region.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
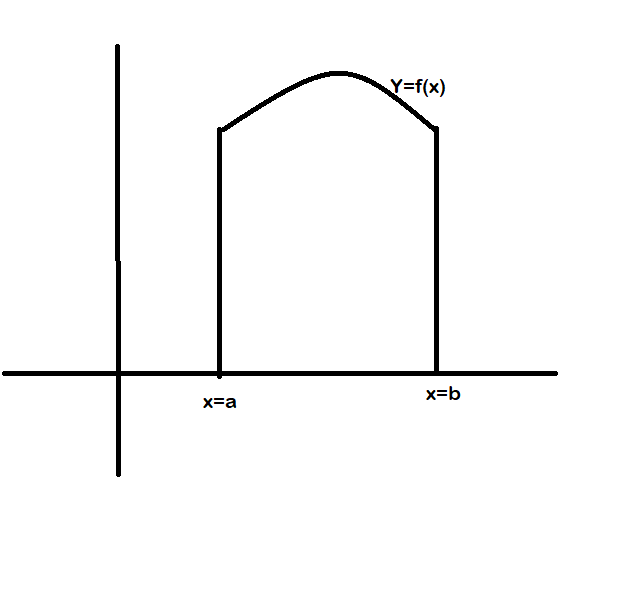
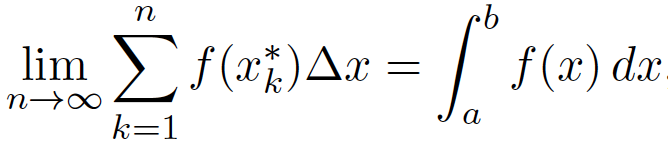
Above, is the picture of the region and the bottom picture is the definition I am working with
Why is it assumed when calculating the area of the shaded region under the curve y=f(x), above the x-axis and bounded between a pair of vertical lines that the function should be both continuous and defined on the closed interval [a,b], there are many restrictions imposed by the definition.
In the following step function, the function is discontinuous at more than one point yet I can compute the area under each horizontal line because the area of the rectangle is given by (b*h)
Why do we divide the interval into n equal subintervals as the base, when we can still construct a rectangular network, in which each rectangle has a different base. And, we can still find the area of the region if we know how to find the area of each rectangle we can then find the area of the rectangular network.
Area of a whole= Sum of the areas of the parts.
How do we find the area of the shaded region if we take its nature of this region to be an upper edge curve?
If one region is contained within another the area of the contained region is less than or equal than that of the containing region.
In other words
Lower Riemman sum<Area of region<Upper Riemman sum
The nature of the inscribed rectangles is different from that of the region, and that's why I don't quite understand why in the limit these two sums are exactly equal to the area below the region.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

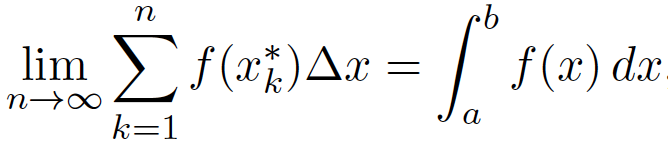
Above, is the picture of the region and the bottom picture is the definition I am working with
1 Answer
So I assume
and
Typically for this kind of definition, we mention that the limit must be exist and be the same for all possible choices of
If
It is not necessary to assume that
Some introductions do add this assumption to their initial definition.
I think it is considered a simplifying assumption by those who use it.
I do not see a "following step function", but I can imagine one. Yes, we can certainly find the area under the graph on a bounded interval. If we drop the continuity requirement, then the new definition of definite integral will apply to a step function also.
The division of the interval into equal subintervals is purely a simplifying method, More generally, we can define a "partition"
We then define
Proofs using this definition seem more complicated to many.
Either way, we are summing the areas of more and more rectangles with smaller and smaller bases on the
The approximation by rectangles gets better and better as the number of rectangles increases. This picture can help with that.
Source: I, KSmrq [GFDL (http://www.gnu.org/copyleft/fdl.html), CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/) or CC BY-SA 2.5 (http://creativecommons.org/licenses/by-sa/2.5)], via Wikimedia Commons

