Derivation of the equation of a Hypocycloid?
https://ocw.mit.edu/courses/mathematics/18-01-single-variable-calculus-fall-2006/assignments/ps3.pdf (question 6)
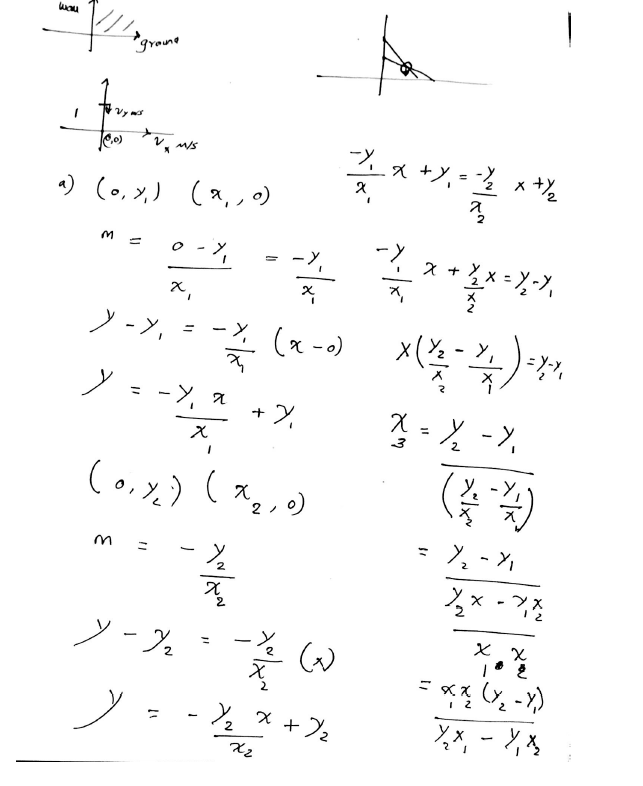

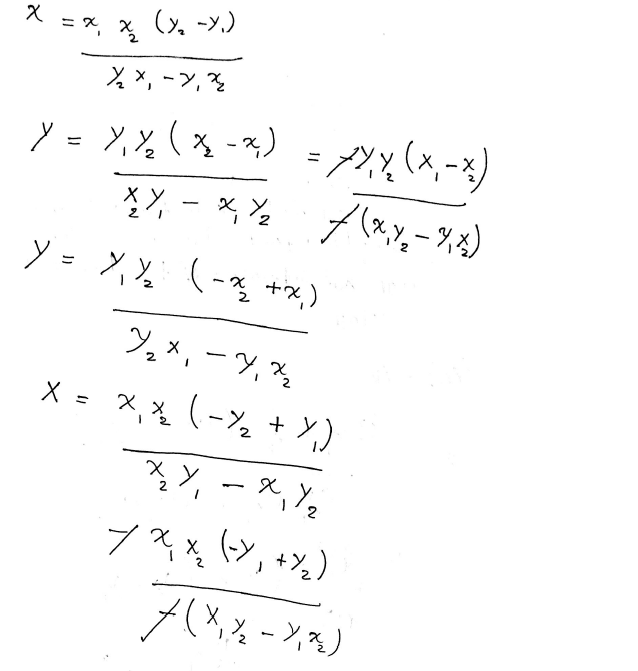
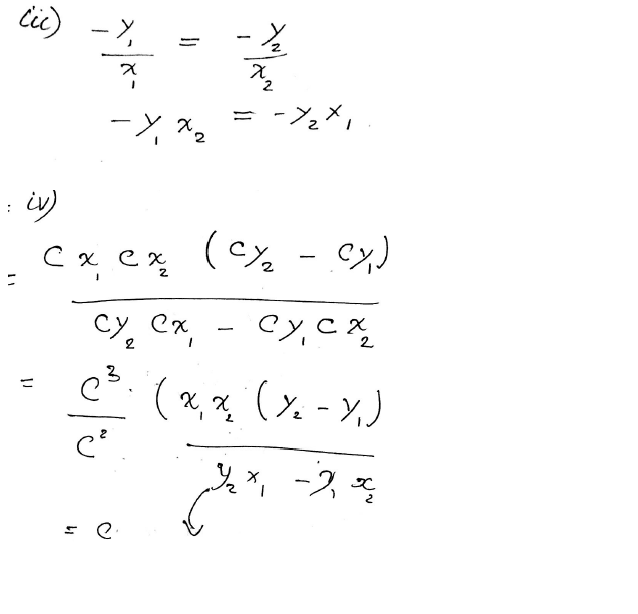
b) The equation involving x2 and y2 that expresses the property that ladder L2 has length one x2^2+y2^2=1 y2=(1-x2^2)^0.5 The equation of the line made by the ladder with its foot at (x2,0) is y=-y2/x2(x-x2)=-(1-x2^2)^0.5/x2(x-x2) After computing the derivative with respect to x2, how can I use the information about the derivative at x2 to know more about the derivative at x1?
dy/dx2=x-x2^3/x2^2(1-x2^2)^0.5
https://ocw.mit.edu/courses/mathematics/18-01-single-variable-calculus-fall-2006/assignments/ps3.pdf (question 6)
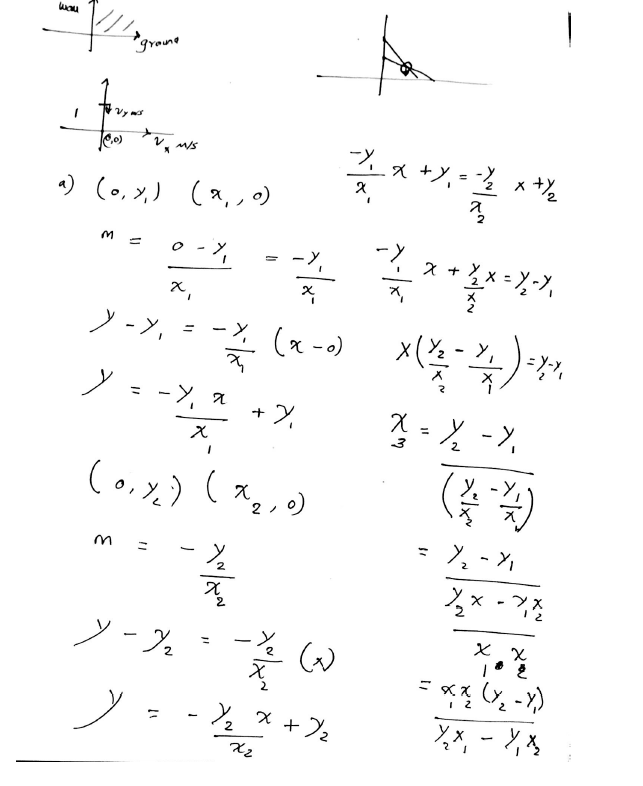

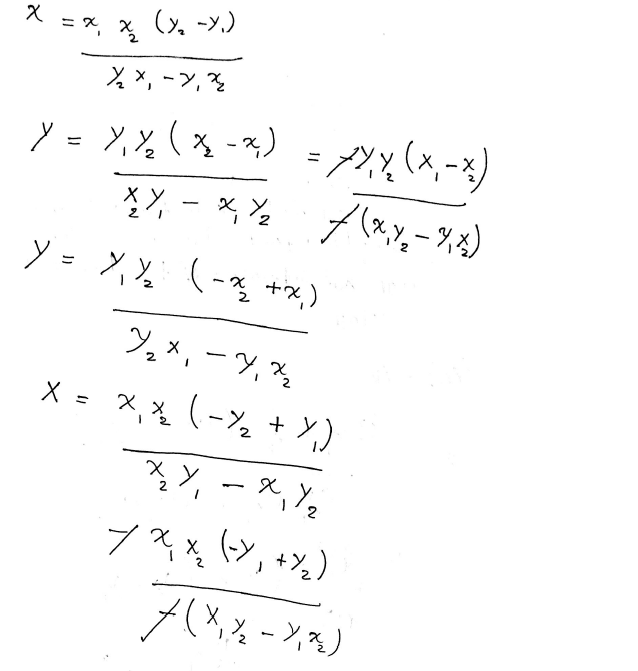
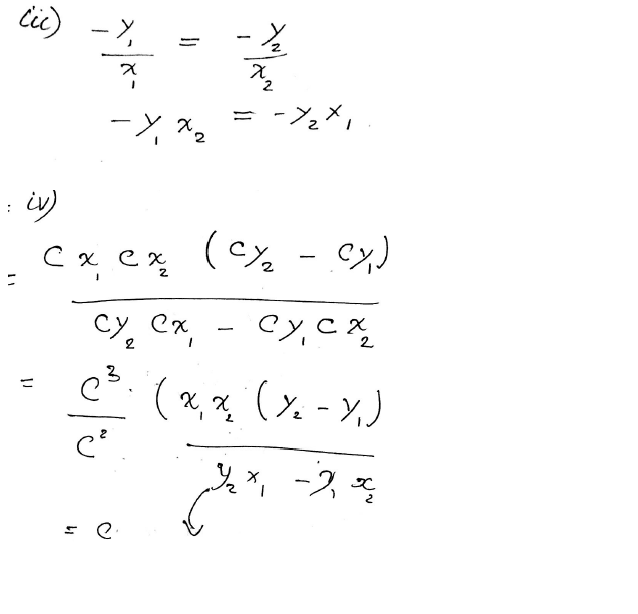
b) The equation involving x2 and y2 that expresses the property that ladder L2 has length one x2^2+y2^2=1 y2=(1-x2^2)^0.5 The equation of the line made by the ladder with its foot at (x2,0) is y=-y2/x2(x-x2)=-(1-x2^2)^0.5/x2(x-x2) After computing the derivative with respect to x2, how can I use the information about the derivative at x2 to know more about the derivative at x1?
dy/dx2=x-x2^3/x2^2(1-x2^2)^0.5
1 Answer
See below.
Explanation:
Calling
and
and defining
we have
for
and the intersection point is
now considering that
now substituting into
now making
Attached the plot of
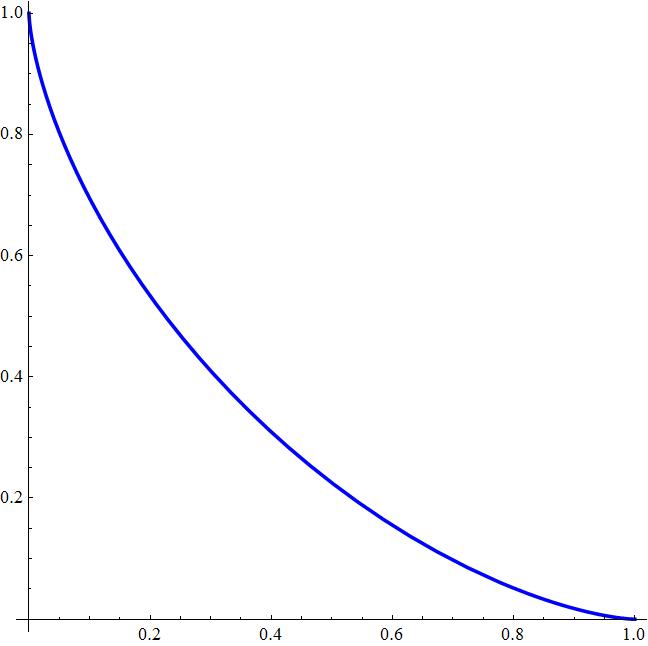
NOTE: This last result can be understood as a parametric description for

