Describe the solid whose volume is represented by #int_(0)^(3) (2pi x^5)dx#. ?
please do this question.
Thank you.
please do this question.
Thank you.
1 Answer
Jul 8, 2017
Recall that a solid of revolution about the
#V = 2pi int_(a)^(b) xr(x)dx# ,where
#r(x)# describes the shape that will be revolved around a vertical axis,#x# indicates the distance of the function's edge to the rotational origin, and#2pi# is the circumference in radians.
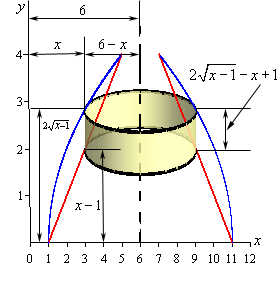
In this case, you have
I assume it is rotated about

