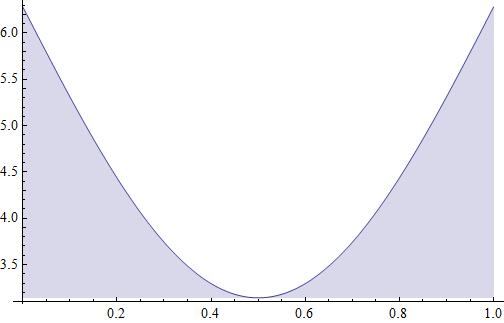
Determine a region whose area is equal to the given limit?

Question

Topic labeling may be inaccurate/incorrect.
This is CALCULUS I. Please apply appropriate methodology and formulae.

Do not evaluate the limit.

(A) #\lim_{n\rarr\infty}\sum_{i=1}^{n}8/n\ln(1+(8i)/n)#

(B) #\lim_(n\rarr\infty)\sum_{i=1}^{n}=\pi/n[\sin(\pi+(i\pi)/n)+2]#

19607 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-03T23:42:20

(A) #11.775021196025975#
(B) #2(pi-1) #

(A)

#sum_(k=1)^n8/n log(1+8 (k/n)) = 8sum_(k=1)^nlog(1+8 (k/n)) 1/n#

When #n->oo# we have

#lim_(n->oo)sum_(k=1)^nlog(1+8 (k/n)) 1/n approx int_0^1 log(1+8x)dx#

where for #k=1,2,cdots,n#

#1/n = Deltax#, #0 < (k/n= k Delta x = x_k) le 1 # and

#lim_(Deltax->0)sum_(k=1)^nlog(1+8 x_k) Deltax = int_0^1 log(1+8x)dx#

So

#8int_0^1 log(1+8x)dx = 11.775021196025975#

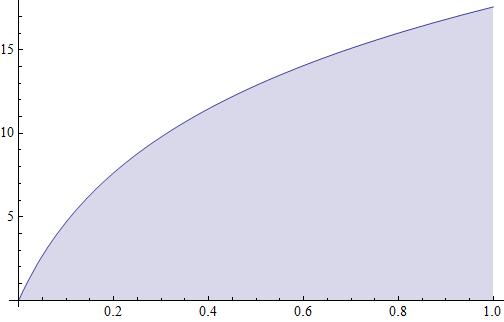
enter image source here

(B)

By the same way

#\lim_(n\rarr\infty)\sum_{i=1}^{n}\pi/n[\sin(\pi+(i\pi)/n)+2] = pi \lim_(n\rarr\infty)\sum_{i=1}^{n}[\sin(\pi+pi(i/n))+2]1/n approx#

#approx pi int_0^1 (sin(pi+pi x)+2)dx =2(pi-1) #

enter image source here