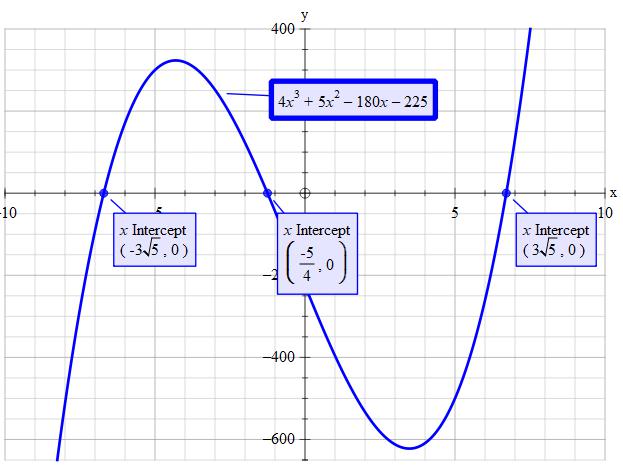
Given: #4x^3+5x^2-180x-225#
Set #4x^3+5x^2-180x-225=0#
#color(blue)("Lets test the "-5/4)#
#4(-5/4)^3+5(-5/4)^2-180(-5/4)-225=0?#
#color(white)("d")-125/16color(white)("d.d") +color(white)("ddd")125/16 color(white)("dd") +color(white)("ddd")225color(white)("ddd.")-225=0 # confirmed
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the factor that is the quadratic")#
#color(brown)("3 options: long division, synthetic division, building it")#
#color(brown)("I chose long division.")#
#color(white)("dddddddddddddd")4x^3+5x^2-180x-225#
#color(magenta)(4x^2)(x+5/4)-> color(white)("d")ul(4x^3+5x^2larr" Subtract")#
#color(white)("ddddddddddddddd")0color(white)("d")+color(white)("d")0color(white)("d")-180x-225#
#color(magenta)(-180)(x+5/4) ->color(white)("dddddddd")ul(-180x-225larr" Subtract")#
#color(white)("dddddddddddddddddddddddddd")0color(white)("d.")+color(white)("d")0#
So no we have: #(x+5/4)(4x^2+0x-180)=0#
Write as: #(x+5/4)(4x^2-180)=0#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the remaining factors")#
Observe that #4x^2->(2x)^2 # and the 180 is negative. So we could use difference of squares.
Write as: #(x+5/4)( color(white)(2/2)(2x)^2-(sqrt(180))^2color(white)(2/2))=0#
#(x+5/4) (color(white)(2/2)2x+sqrt(180)color(white)(2/2))(color(white)(2/2)2x-sqrt(180)color(white)(2/2))=0#
but
#180=2^2xx3^2xx5 color(white)("dd")#
Thus #color(white)("dd")sqrt(180)color(white)("dd")=color(white)("dd")2xx3xxsqrt5color(white)("dd")=color(white)("dd")6sqrt5# giving:
#color(white)()#
#(x+5/4) (color(white)(2/2)2x+6sqrt(5)color(white)(2/2))(color(white)(2/2)2x-6sqrt(5)color(white)(2/2))=0#
Both #2x# and #6sqrt5# can have 2 factored out giving:
#2(x+5/4) (color(white)(2/2)x+3sqrt(5)color(white)(2/2))(color(white)(2/2)x-3sqrt(5)color(white)(2/2))=0#
The zeros are #-5/4, +3sqrt5 and -3sqrt5#