Determine the relationship between the rates of change of f and g. ?

The equation represents the function f, and the graph represents the function g.

f ( x ) = 6x - 5

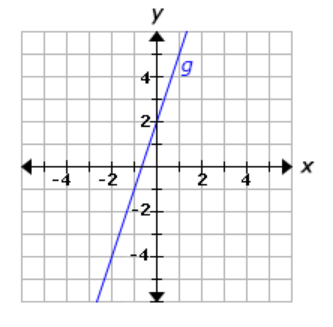
enter image source here

Determine the relationship between the rates of change of f and g.

  • The rate of change of g is twice the rate of change of f.

  • The rate of change of f is the same as the rate of change of g.

  • The rate of change of f is 3 times the rate of change of g.

  • The rate of change of f is twice the rate of change of g.

1 Answer
Ananda Dasgupta
Jun 19, 2018 
The rate of change of f is twice the rate of change of g.

Explanation:

The rate of change of #f# can be found from the given expression for #f#. This shows that

#(df)/dx = d/dx (6x-5) = 6#

To find the rate of change of #g#, we have to use two suitable points on the graph (as the graph is a straight line, any pair should return the same value for the slope). It can be seen that the graph for #g# goes through the points #(-1,-1)# and #(1,5)#. Thus the rate at which #g# increases is

#(5-(-1))/(1-(-1)) = 6/2=3#

Related questions
Impact of this question
2434 views around the world
You can reuse this answer
Creative Commons License