In order for a function f(x) to be continuous at some value x = b, the following three conditions must be true at the same time:
{(f(b) " exists"), (lim_ {x->b} f(x) " exists"), (lim_ {x->b} f(x) = f(b)) :}
For this problem, the b value of interest is x = -5. To make the function continuous at x = -5 we need to handle each of these conditions in turn.
Function is defined at -5
The first condition is that f(-5) exists. This is a particularly easy one to satisfy; since we are told that f(-5)=a (whatever we find that a to be), we know that f(-5) will exist.
Limit is defined at -5
This one can be proven by at least two different means, depending on your knowledge of Calculus. Given the question (implied to be an early level of Calculus), the L'Hopital's Rule method is unlikely to be known (but provides a very quick way to find the limit once you learn it later!). Instead, we will use factoring and cancellation to find the limit:
lim_ {x->-5} f(x) = lim_ {x->-5} (x^2+6x+5)/(x+5)
= lim_ {x->-5} ((cancel(x+5))(x+1))/cancel(x+5) = lim_ {x->-5} (x+1) = -4
Thus, we've determined that the limit at x = -5 exists and is found to be -4.
Limit must equal the function value at -5
Now that we've found the limit at -5, and we know that f(-5)=a (as noted in the problem), we can satisfy the third requirement by ensuring that the limit at -5 equals the function at -5, or:
lim_ {x->-5} f(x) = f(-5)
-4 = a
This, a should be -4 for the function to be continuous at x=-5. A look at the graph of f(x) shows visually why this needs to be done:
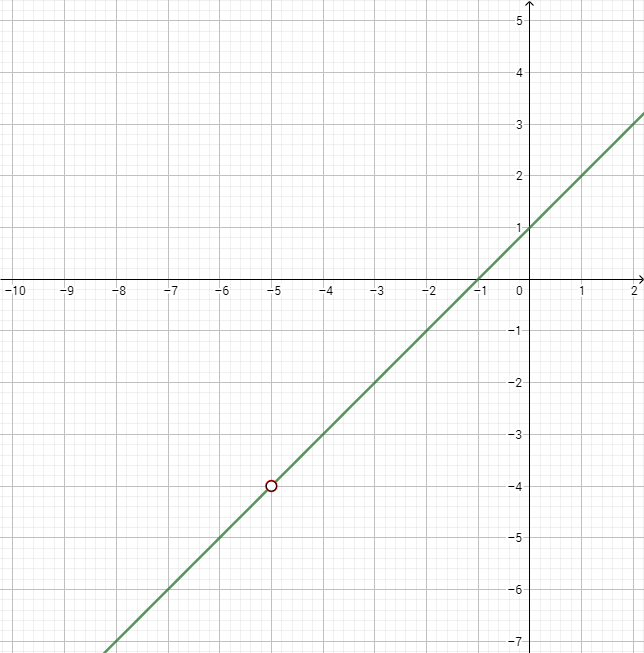
The graph looks like a straight line, and that comes mainly from the work we did during the limit calculation; if x!=-5, then we are "allowed" the factor and cancel as we did in the limit calculation, which leaves behind (x+1), a straight line with slope of 1, as you see in green.
The "hole" in the graph at x=-5 is the place where f(x) was originally not defined, and it seems visually clear that to "fill" or "plug" that hole we need to drop a point at (-5,-4), which is what mathematically we did by defining a to be -4. This is what is referred to as a "removable discontinuity", by the way.

