Displacement from origin?
An object is displaced by 60.0m at a bearing of 60.0∘. If the object then moved 30.0m due north, what is the final magnitude of displacement of the object from its origin?
An object is displaced by 60.0m at a bearing of 60.0∘. If the object then moved 30.0m due north, what is the final magnitude of displacement of the object from its origin?
2 Answers
Explanation:
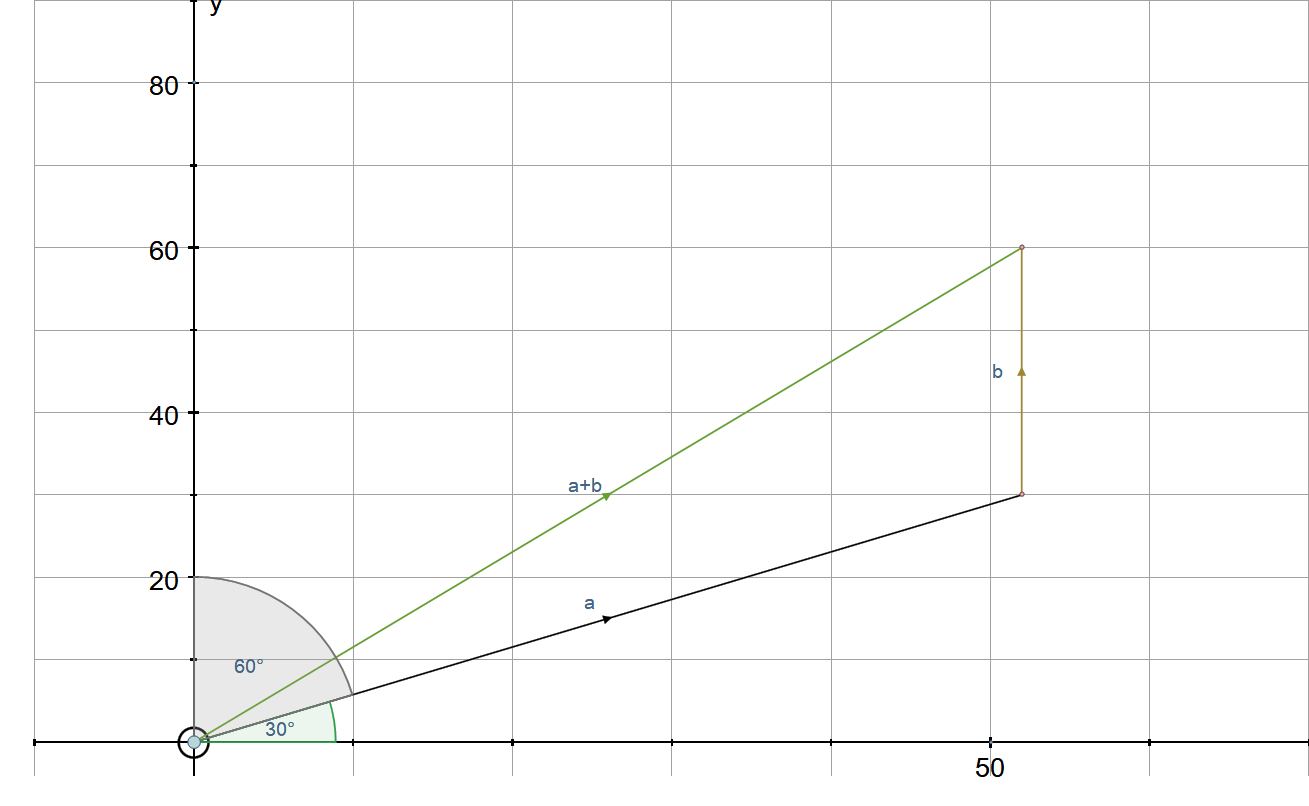
I am taking the bearing of
We will call this vector
Using cosine and sine functions:
Due north is
Calling this
Displacement from origin is:
Explanation:
I made up these sketches of the 1st and 2nd locations of the object due to these displacements.
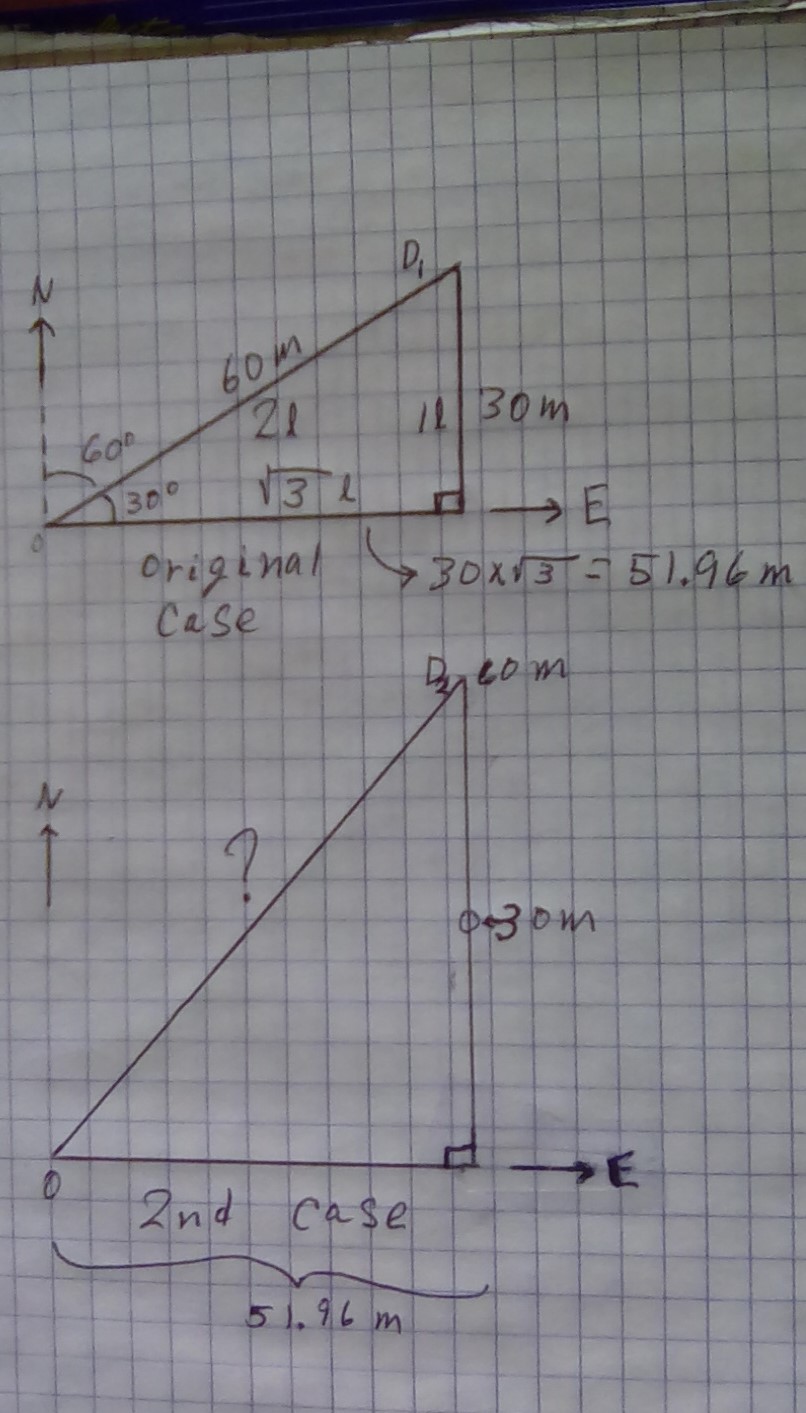
The origin is bottom left, marked
Look at the triangle of Case 1. The direction of the displacement was
Basic details about the relative lengths of the sides of a 30-60-right triangle:
- If you consider the length of the side opposite the
#30^@# angle to be 1 unit, call it#1l# , then the length of the hypotenuse will be#2l# . - The length of the 3rd side is
#sqrt(3)""l# or#1.732l# . (I marked those relationships inside the 30-60-right triangle.)
We know that the length of the hypotenuse is 60 m. Using the above details about 30-60-right triangles we can say that the side opposite the
Now look at the triangle of Case 2. It is not a 30-60-right triangle. But we know 2 of the sides: the horizontal side is still 51.96 m and the vertical side is
Those 2 dimensions, and Pythagoras, allow us to find the final magnitude of displacement of the object from its origin.
I hope this helps,
Steve


