Question

Distances from Zagreb to Vienna is 400 km. At the same time, the first train goes from Zagreb with the speed of 100 km/h and the second train from Vienna goes 120 km/h. How to calculate the meeting spot graphicaly?

Answer 1

See the graph made,here the red line is for the train going from Zagreb to Vienna and blue line for the train going from Vienna to Zagreeb.

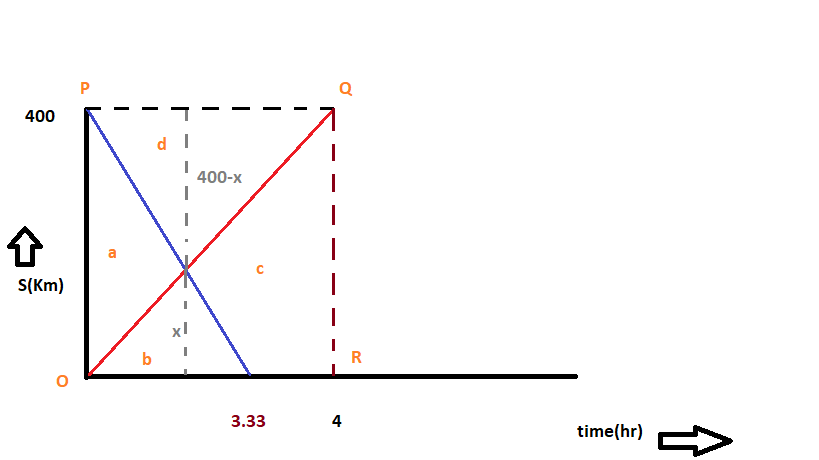
So,equation for the 1st train is `s=100t` and for the 2nd `s=120t`

So,the 1st train reaches Vienna in time `t=400/100=4 hrs` and the 2nd train reaches Zagreeb in time `t=400/120=3.3 hrs`

Now,we have got a meeting point of the two staright lines in the graph.The two lines divide the whole area `PQRO` in to `a,b,c,d`

Let,draw a perpendicular line from it on time axis,if its length is `x` then the extension of this very line above on a line parallel to time axis is `400-x`

So,we can say,area of the whole rectangle is `400*4=a+b+c+d`

or, `1600+b =(a+b) +(b+c) +d.......1` (adding `b` to both sides)

from the diagram, area under the curve by blue line is `a+b=1/2*3.33*400`

and area under the red line i.e area of triangle `OQR` is `b+c =1/2*4*400`

`d=1/2*4*(400-x)`

and, `b=1/2*3.33*x`

Put the values in the equation `1` you will get, `x=181.72Km`

this is the meeting point calculated from Zagreeb towards Vienna.

Answer 2

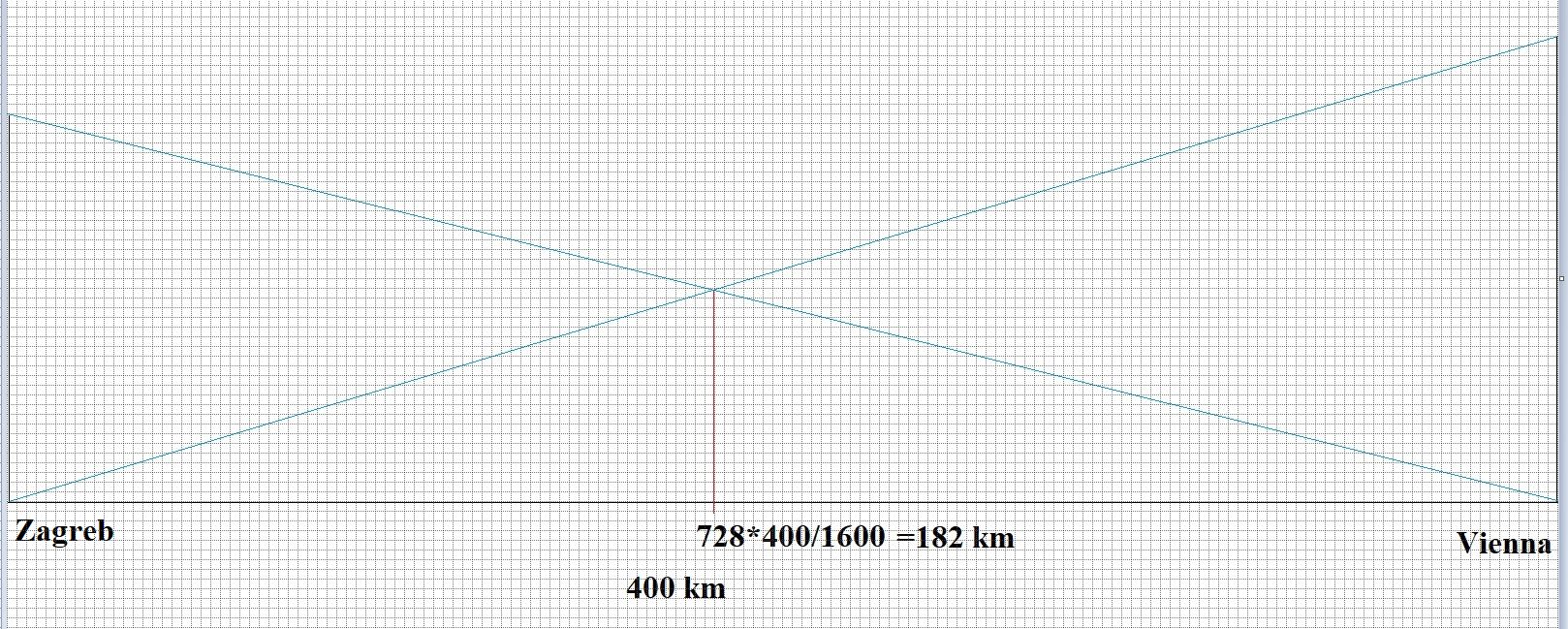
1. Let origin represent Zagreb.
2. Select a scale to represent distance between Zagreb and Vienna on the `x`-axis which is given to be `=400\ km`.
   In the graph I took `4` small divisions `=1\ km`.
3. Select proportional scale to represent along `y`-axis speed of train.
   I selected `4` small divisions `=1\ kmh^-1`
4. Plot speed of train from Zagreb to Vienna at the origin given as `100\ kmh^-1`.
5. Plot speed of train from Vienna to Zagreb at the point representing Vienna given as #120\ kmh^-1
6. Join tip of speed of first train with point Vienna.
7. Join of tip of second train with origin, representing Zagreb.
8. Drop a perpendicular on `x`-axis from the point of intersection lines drawn in steps 6 and 7.
9. Read number of divisions from origin where this perpendicular meets the `x`-axis. State the distance of this point of intersection from Zagreb.

I found out with the help of enlarged view, facility available in MS Paint, the number of division `=728`. This corresponds to a distance of `182\ km.`

.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-

Verification with the help of Arithmetic.

Let the train meet after time `t`.
Distance covered by train 1. from Zagreb to Vienna `=100t\ km`
Distance covered by train 2. from Vienna to Zagreb `=120t\ km`

Once these meet sum of distances covered by each train is equal to distance between the two cities.

`:.100t+120t=400`
`=>t=400/220=20/11hr`

Distance from Zagreb where trains meet`=100xx20/11=181.bar81 \km`

Correct within accuracy of the graphics tool.