Question

Do solid particles vibrate?

Answer 1

Yes. And in lattices, if the atoms themselves are heavier, they vibrate at lower natural frequencies, and vice versa.

---

This can be modeled by an infinite array of harmonic oscillators, i.e. balls and springs.

For simplicity, consider a segment of a 1D lattice of `N` identical atoms vibrating with a given wave number `kappa` over time `t`, with the atoms at each end fixed:

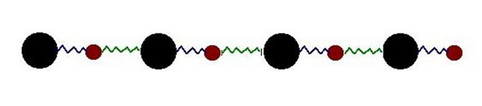
The position over time for the `j`th atom is given by:

`x_j(t) = A_(kappa) e^(i(omega_(kappa)t + kappa aj))`

They would vibrate with an angular frequency `omega_(kappa)` of:

`omega_(kappa) = 2sqrt(k/m)|sin((kappa a)/2)|`

and, since `0 <= |sinu| <= 1`, they would reach a maximum frequency, called the Debye frequency `omega_D`, of:

`omega_D = 2sqrt(k/m)`,

where:

• `k` is the force constant between the two identical atoms in `"kg/s"^2`.
• `kappa` is the wave number (the number of waves for a unit distance).
• `m` is the mass of each atom in `"kg"`.
• `a` is the position coordinate of a given atom.

Above `omega_D`, the vibrations in the lattice become independent of the lattice, i.e. the atoms in each unit cell vibrate at a well-defined frequency that is distinct from the collective lattice vibrations.

In other words, the wavelength `lambda` is lower than the width of the unit cell, given by the Debye (minimum) wavelength `lambda_D`.

A full derivation of the above equations can be found here using differential equation math and Lagrangian mechanics.