Do we create maths or do we discover it?
Is mathematics an art or a science? Is ZZ the work of God and all else that of man? Do numbers exist out there in the ether? Or is it merely a way to view the world through the guise of an axiomatic system of logic? Your input...
Is mathematics an art or a science? Is
4 Answers
Yes.
Explanation:
“Maths” are a human creation that seeks to make sense (order, logic) out of the observable universe. Thus, we “discover” mathematical principles in nature, but the actual expression of them as maths is a human creation.
The study of maths progresses continuously a we discover more phenomena and create more logical connections and equations (maths) from our new observations and continued study of past formulations and explanations.
Maths may be considered the “language” of Natural Philosophy (Science).
It depends...
Explanation:
One of the essay questions I faced about 38 years ago on a university entrance paper was to answer "Is mathematics an invention or a discovery?". The university concerned seemed to like my answer, which essentially boiled down to distinguishing between the symbols we use as language to describe mathematics - which I identified as an invention - and mathematics itself, which I argued was a discovery.
For example, regardless of the symbols you use for counting numbers, the (mathematical) property
When I described what I had written to a contemporary, he described me as a Platonist.
Whether you follow Plato or not, it seems to me that the relationships between mathematics and the "real world" are on the basis of abstractions and modelling. Numbers do not "exist" in the "real world". They and other mathematical objects can be used to describe models of the "real world".
What we do find is that if we choose a set of axioms and rules for derivation from them, then we observe various consequences. If our derivation is rigorous, then the result is deterministic - it will always be 'true' in the context of those axioms and associated rules.
As a result, if we so choose, then we can say that mathematics exists in the sense that those consequences exist ready to be discovered once you choose the axioms and rules.
To add a little depth to these considerations, it may be helpful to look at the case of classical ZFC set theory and the continuum hypothesis (CH). The continuum hypothesis basically says there are no distinct infinite cardinals strictly between the number of integers and the number of real numbers.
The axioms of ZFC provide a rich foundation for understanding sets and the ability to prove all kinds of interesting results. However, neither CH nor
To me, the natural question is: "Is the continuum hypothesis true?"
The uncomfortable truth seems to be that you can choose.
Mathematical symbols are a created framework that allow us to discover unchanging mathematical relationships in nature.
Explanation:
An idea that pops up when I read this question is the ideas of Plato/Socrates. In essence, they thought that if you wanted to understand something - a tree, for instance - you had to understand the tree completely. You had to know what it was made of, what it did, how it operated in the world... everything.
Since it is impossible to have complete knowledge of something, humans devise ways of knowing certain elements about things. We may not have complete understanding but we can get as close as we can.
In the world of gaining understanding, we can reach for different kinds of tools. One set of tools deals with things that are unchanging - and it's here that we enter the world of mathematics and science. A 1 is a 1 is a 1.
And so to the question of maths - do we discover them or do we create them?
We certainly made a system, a framework, to shape our knowing. That is created. But before the trig ratios were found to exist, they did exist, waiting to be found - discovered.
And so the system we use is created to help us discover new knowing within the field of Total Understanding. Put another way - we can change the system and the symbols - the created bits. But whatever it is we do to the created portion of mathematics, the relationships and ratios that exist within the world won't change - the discovered bits.
I love this question, but I cannot give a simple, short answer to it. In part this is because I am not sure what to say about it. Here are some of my thoughts (for whatever they are worth).
Explanation:
My answer to this question is closely connected with my views on the nature of mathematics.
The following views are mine and I could be mistaken.
Mathematics involves the description and study of relationships and patterns. So the question becomes: Are relationships and patterns independent of an observer?
I see mathematics (and much of non-mathematics) as arising from the notion of sameness or similarity of various kinds.
We (human observers) recognize a kind of sameness.
Imagine a young child being asked, "Which one of the things underneath is like the thing at the top?"
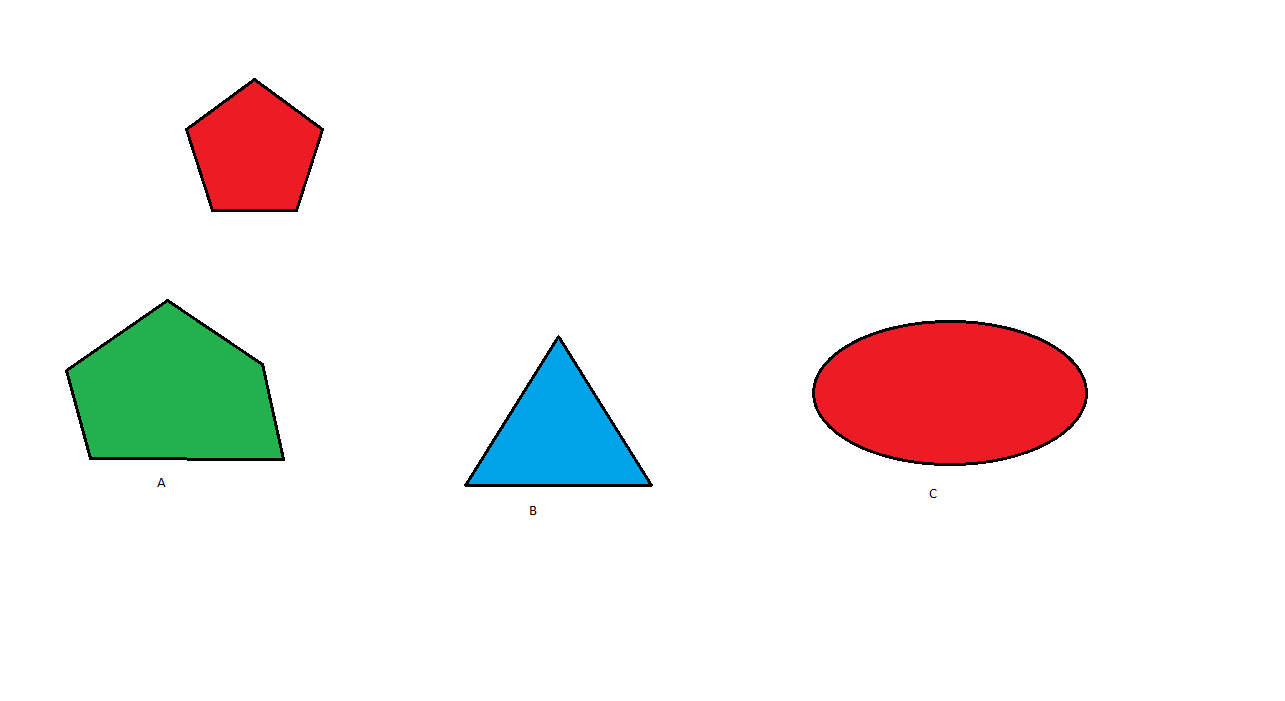
Even without names for shapes and colors (and number of sides) we can imagine a child picking one (or two) as being "like" the red pentagon.
From this simple beginning I imagine we develop words for the sameness between the sample and A (five sided), the sample and B (regular shapes), the sample and C (red). Later we group ways of being alike into classes: shape, straight line shape, color (I have neglected a size difference, but we could add a giant red pentagon.)
This is a generalization of the foundations of transfinite numbers. We define the notion of "same cardinality" before we define a cardinality or a cardinal number. "Sameness", "similar", "alike", "the same (in some way"" takes precedence over saying what way things are the same. I take "same color" to be more fundamental than having a "color" (or "being red").
In a similar imaginative story, I can picture early humans having a hand sign for deer, perhaps (or eventually) with a sign for question and later still for "how many". The answer is not a word or what you and I would call a number, it is holding up a corresponding number of fingers (or sticks or a pile of stones). One-to-one correspondence precedes numbers.
I imagine the origins of mathematics to be like these stories.
No, I'm not sure that my stories are accurate, but I find them plausible.
Now the question for me becomes:
To what extent are these similarities ("samenesses"?) independent of an observer?
I feel a need to turn to the animal psychologists to ask them whether other animals parse the world into similar and different in the same ways as humans.
(I would guess not. Dogs do a lot of parsing by scent, perhaps less by color.)
In addition to wondering about that, I wonder about this with regard to numbers:
We have an intuition that there are either 5 deer in the field or there are not. But what counts at "the field"? More generally, without an observer to identify a set and set membership, do sets exist? Is there a set of planets orbiting our sun? How many elements does it have? Does the answer depend on an observing deciding what counts as a planet? (I think it does.)
There is an example that makes me think that an observer (human) is not needed to generate the kind of sameness that leads to numbers. I know essentially nothing about biology, but I do know that either the number of chromosomes of two animals matches or it doesn't match. This is true regardless of an observer deciding what counts as a chromosome or what counts as animals or anything else.
This makes me think that the counting numbers are "out there" independently of us observing them.




