Does #a_n=x^n/(xn!) # converge for any x?
2 Answers
converges for
Explanation:
Using the Stirling asymptotic approximation
The sequence converges if
then the convergence is attained for
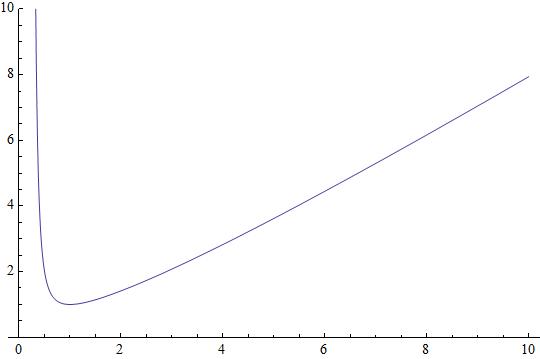
The function
Attached a plot of
Yes,
Explanation:
Choose any real number
Let us look at
So, we have
By Squeeze Theorem,
which implies
I hope that this was clear.


