Does atmospheric pressure affect the vapor pressure of a liquid?
1 Answer
Sure... but more often than not, we ignore such influences.
Vapor pressure of a liquid is a function of temperature. As can be seen on any phase diagram, temperature varies independently from atmospheric pressure... They are the
Consider the phase diagram of water:
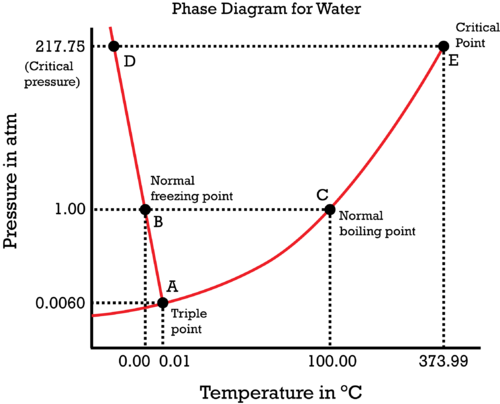
The vapor pressure, while it changes with atmospheric pressure, is really dependent on temperature to a first approximation, as given by the Clausius-Clapeyron equation:
#ln(P_(vap2)/P_(vap1)) = -(DeltaH_(vap))/R[1/T_2 - 1/T_1]#
Vapor pressure is marked by the
- Let us begin at
#"B"# (water at#0^@ "C"# ) and move horizontally towards#"C"# (water at#100^@ "C"# ); that is generic heating of water to reach the boiling point. As this occurs, the vapor pressure is increasing along the#color(red)"red curve"# . - We then attempt to cross the
#color(red)("liquid-vapor coexistence curve")# ,#bar"AE"# while boiling. At this point, the pressure of the vapor above the liquid has already become equal to the#"1.00 atm"# atmospheric pressure.
And in all this, regardless of what atmospheric pressure we are at, the shape of the
The vapor pressure is hardly influenced by the atmospheric pressure in that regard, because we ignore the intermolecular forces in ideal vapors.
When we discuss real gases, which have attractive and/or repulsive intermolecular forces (as determined by the compressibility factor
Those use, e.g. the van der Waals, Redlich-Kwong, Peng-Robinson, etc. equations of state.
Only then is an influence of atmospheric pressure on vapor pressure in question, since we would allow the surrounding atmosphere gases to interact with the vapors above the liquid.
More often than not, we ignore such influences.

