Does entropy increase or decrease during transformation of egg into chicken?
1 Answer
Considering the egg from the standpoint of statistical thermodynamics, it increases.
However, when including the negative entropy contribution from gene expression required to sustain growth into a chick, the overall entropy is proposed by Sanchez to decrease.
Explanation:
Definition of entropy can be ambiguous in terms of conceptualization. The "degree of randomness" part is really hard to visualize without further defining what "disorder" is.
GENERAL ENTROPY DESCRIPTION
In plain sight, a hen-chick might look more "regular" than an egg, given that it is more solid. But, there are several points to consider:
- If you consider origin (0,0,0) and sprinkle some dots randomly around it, (at a constant
#r# lets say), after many attempts that will be a sphere. Now do it for random#r# 's and you will find a blurred spherical structure, like:
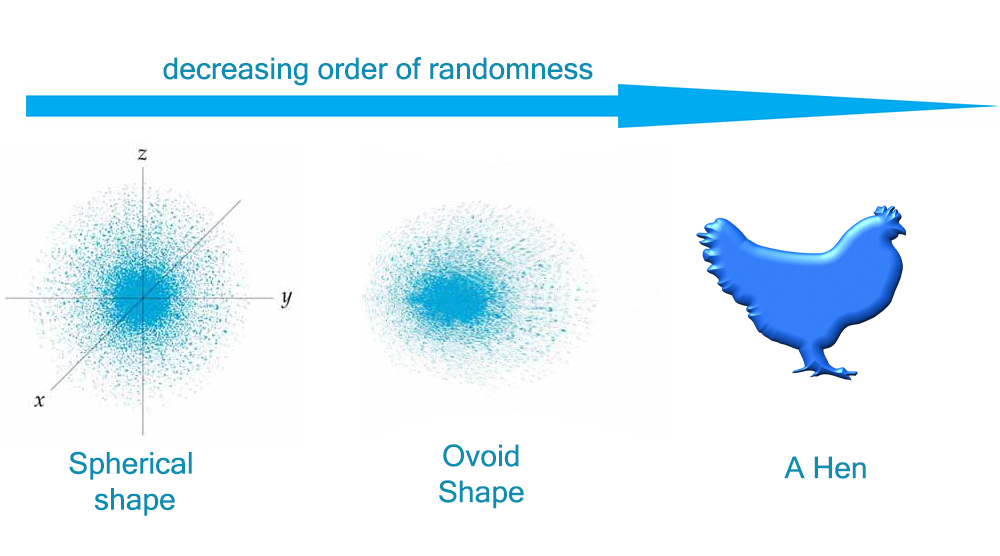
We have just defined the probability density of an egg (ovoid) over time, but a chick's probability density is less well-defined (harder to plot).
Hence, the chick has potential for being more entropic from a traditional disorder (with respect to quantum mechanics) point of view.
Also, considering the molecular protein structures in egg, they are pretty simple. But they form much more complex proteins in the process of embryological development.
Here, we see that the entropy according to non-biological considerations increases from egg to chick, given the increase in complexity of the proteins. Let us call this
By the Second Law of Thermodynamics,
The egg always releases heat and the mother absorbs the heat from the egg slowly so that the egg is continuously at equilibrium. And if there is not the mother (or, an incubator, which does the same thing), the egg quickly releases the heat, making the developmental process impossible.
TACKLING THIS WITH STATISTICAL MECHANICS
Next, let's consider what is known as Boltzmann's definition of entropy:
#S = k_\text{B} \ln \Omega# ,
where#k_\text{B}# is the Boltzmann constant and#Omega# is the number of "microstates" consistent with the given macrostate observable.
Microstates are the number of ways you can think of a system can be rebuilt keeping the same observed macrostate same. Lets say, you have a house, and all the permutations of the bricks will always leave you with the same house (the macroscopic observables must be the same). So, your house is an "ensemble average" of all these microstates, for a given macroscopic observation of the house.
What happens to our egg
Our system is an almost perfect grand canonical ensemble, it allows heat exchange particles (mostly
The number of microsystems accessible to an egg are less than that are accessible to the chick. The molecules in an egg being simpler, this leaves relatively fewer ways to arrange the atoms to return the same egg macrostate.
Whereas, a chick, with lot more complex proteins etc., has more microstates for a given macrostate of the chick (whether alive or not!).
Thus, the non-biological component to the entropy of the egg (without considerations for sustaining embryonic growth), as we called
Again, this assumes that the egg is not living.
CONSIDERING ENTROPY DUE TO GENE EXPRESSION
Now, we must also include the biological component to the entropy; that is, the entropy due to gene expression required to sustain growth of the egg.
As it turns out, Sanchez proposes at the end of his paper, though his "attempt [is] admittedly crude" (his words), it is sufficient to establish that the entropy due to gene expression, which he calls
Halfway through the paper, he states that:
#DeltaS_"living" = DeltaS_"class" + DeltaS_"gene" < 0#
or in the notation used in this answer:
#color(blue)(DeltaS_"egg"^"chick" = DeltaS_"dead egg" + DeltaS_"gene" < 0)#
That is, the entropy due to gene expression necessary to sustain the chick's life as it gets born is negative enough that the overall entropy difference between the egg and the developed chick (