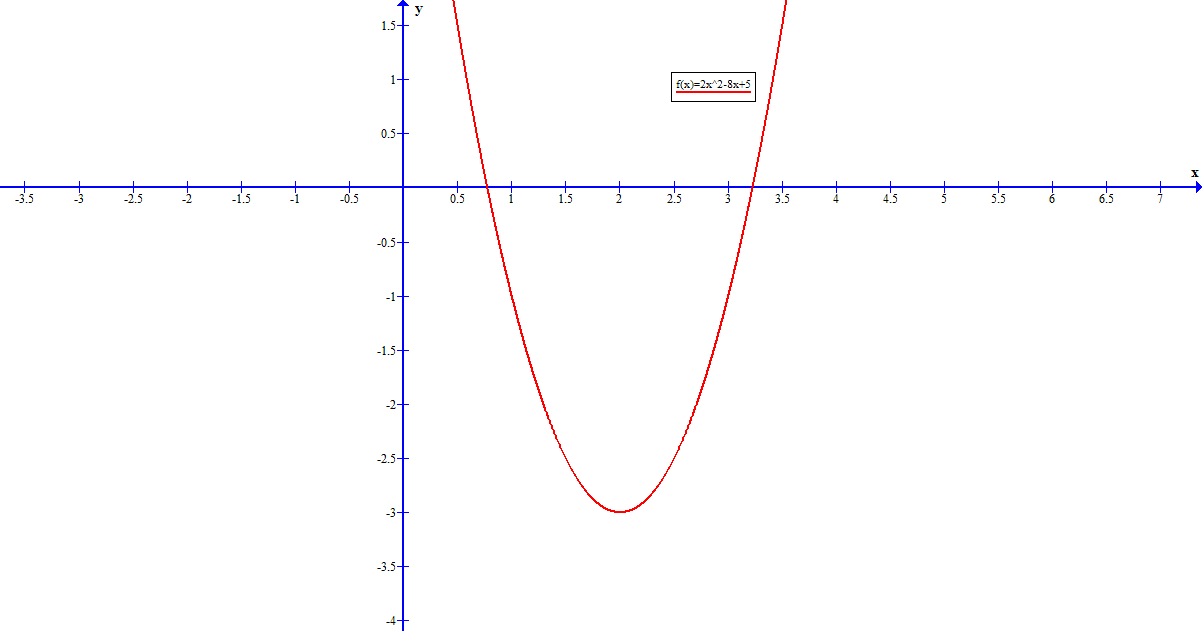
Does #f(x)=2x^2-8x+5# have a maximum or a minimum? If so, what is it?

Question

10332 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-06T12:30:10

#f(x)=2x^2-8x+5# has a minimum value of #(-3)# at #x=2#

A parabola with expressed in the form: #color(red)ax^2+bx=c#
has a maximum if #color(red)(a) < 0#
or a minimum if #color(red)(a) > 0#

#f(x)=color(red)2x^2-8x+5# must, therefore, have a minimum.

The minimum will occur when the tangent slope is #0#;
or expressed in another way, when the derivative of #f(x)# is equal to #0#

#(df(x))/(dx)=4x-8#

and #4x-8=0#
when #x=color(blue)2#

#f(x=color(blue)2) =2 * color(blue)2^2-8 * color(blue)2 + 5#
#color(white)("XX")=8-16+5#
#color(white)("XX")=-3#

enter image source here