Does the formula pr = bh apply to inscribed circles in quadrilaterals? or only triangles?

1 Answer
Hammer
Jun 17, 2018

It depends. But if #r# is the inradius, #p# is the semiperimeter and #S# is the area,

#pr=S#

is true for any tangential polygon.

Explanation:

Before proving this, note that a tangential polygon is any convex polygon which can have an incircle.

This is an example of a tangential polygon:

https://en.wikipedia.org/wiki/Tangential_polygon

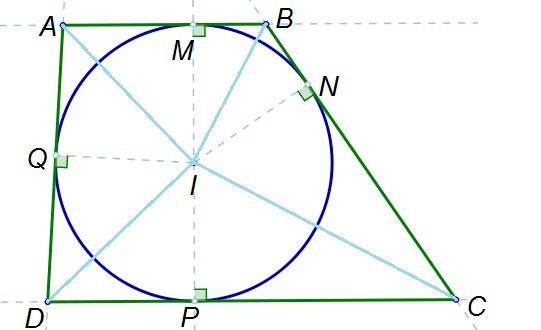
Because the sides of the polygon are tangent to the circle the line that goes through the incenter, #I#, and through the point where the side is tangent, is perpendicular to the respective side.

Now, what we have visualised is a particular case, where the polygon is four sided. Still, let's solve this first.

Let #M#, #N#, #P# and #Q# be the points of tangency.

Notice how the area, #S#, can be written as the sum of the areas of the triangles:

#S=S_(DeltaAIB) + S_(DeltaBIC) + S_(DeltaCID)+S_(DeltaDIA)#

The simplest formula of the area of a triangle is:

#"Area"=("base"xx"height")/2#

If we take the bases to be the sides of the polygon, then the heights will be the inradii:

#S=(ABxxIM)/2+(BCxxIN)/2+(CDxxIP)/2+(DAxxIQ)/2#

#S=(AB*r + BC*r+CD*r+DA*r)/2=r(AB+BC+CD+DA)/2#

We know that, by definition,

#p = (AB+BC+CD+DA)/2#

#:. S = rp#

The general case is solved analogously. If #A_1#, #A_2#, ..., #A_n# are the vertices of a tangential polygon with #n# sides and #T_1#, #T_2#, ..., #T_n# are the points of tangency, then the area of the polygon can be written as:

#S=S_(DeltaA_1IA_2)+S_(DeltaA_2IA_3)+...+S_(DeltaA_(n-1)IA_n)#

#S=(A_1A_2xxIT_1)/2+(A_2A_3xxIT_2)/2+...+(A_(n-1)A_nxxIT_n)/2#

#S=(A_1A_2*r+A_2A_3*r+...+A_(n-1)A_n*r)/2#

#S=r(A_1A_2+A_3A_4+...+A_(n-1)A_n)/2=rp#

Related questions
Impact of this question
1566 views around the world
You can reuse this answer
Creative Commons License