Does the series converge or diverge? Use the integral test.
I am confident that the given series #sum_(n=1)^oo(1/2^n)# converges, but I do not know how to prove this by using the integral test.
I am confident that the given series
1 Answer
Please see below.
Explanation:
.
In order to prove that this series converges, using the integral test, we need to first prove that the integral of this function converges. The reason for that becomes clearer when we look at the graph of this function as shown below.
As you know, the integral of this function evaluated between specified limits gives us the area under the curve.
The difference between the Sum and the integral is that, in the case of the Sum,
As a result, calculating the area under the curve, using the Sum, results in areas of a number of rectangles under the curve and adding them together, which leaves chunks of the area under the curve unaccounted for. And the number of rectangles are much fewer than in the case of the integral.
But the integral does that in a continuous manner and give us the exact area because it takes all values of
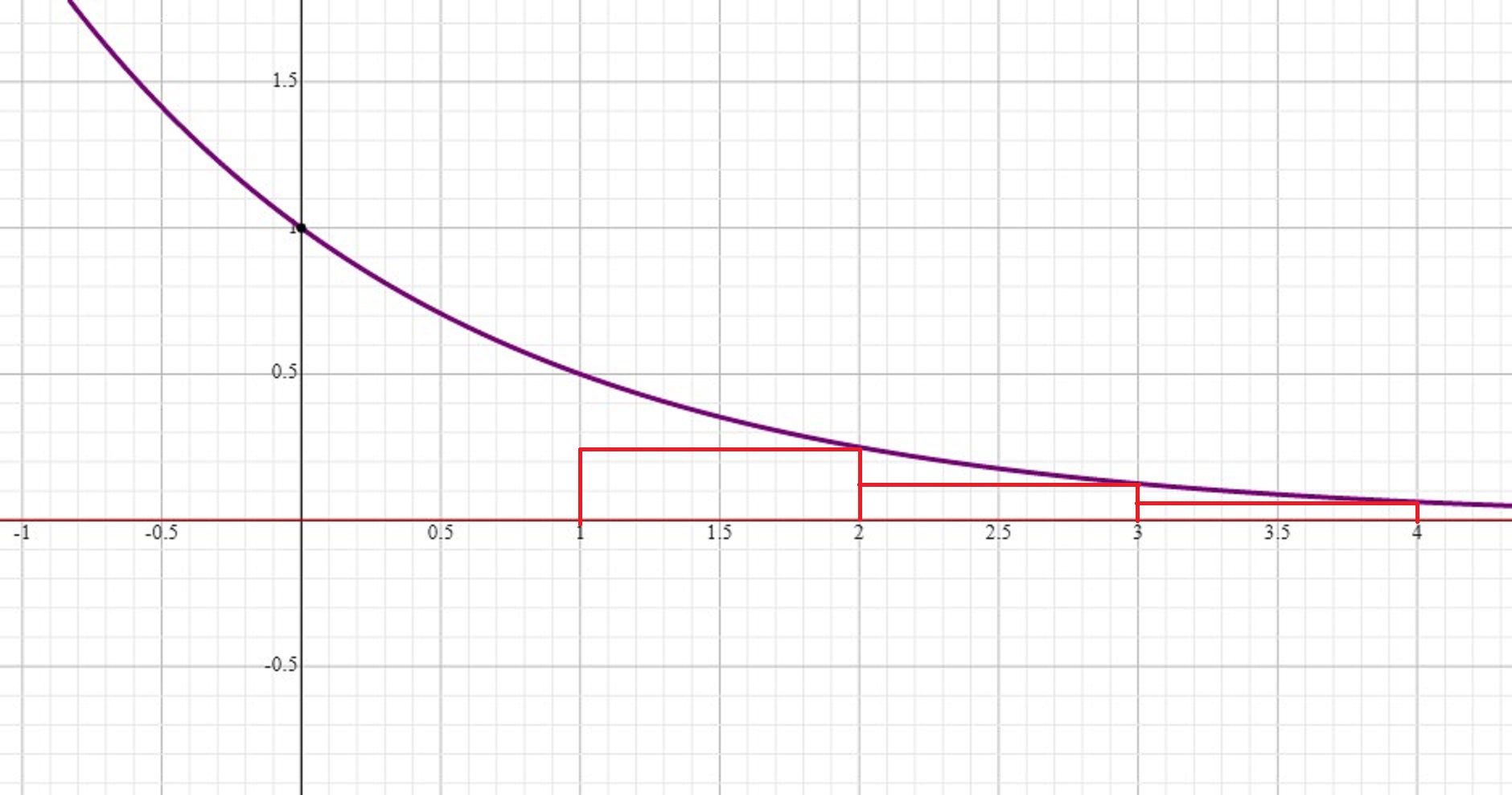
This is the graph of the function
But if we integrate the function and evaluate it between
If we can prove that the integral converges, i.e gives us a finite value for the area, we will prove that the Sum definitely converges because it is always smaller that what the integral gives us. Let's calculate the integral:
Let
Applying the exponential rule:
Now, we substitute back:
As you see, this is a finite value for the area. Therefore, the integral converges. As such, the Sum definitely converges.

