Given a line
#L_1->p=p_1+lambda_1 vec v_1#
and two points #p_a# and #p_b# not pertaining to #L_1# and not perpendicular to #L_1#
for #p in L_1# we have
#norm(p-p_a)=norm(p-p_b)# or
#norm(p_1+lambda_1 vec v_1-p_a)^2=norm(p_1+lambda_1 vec v_1-p_b)^2# or
#norm(p_1-p_a)^2+2lambda_1 << p_1-p_a, vec v_1 >> +lambda_1^2 norm(vec v_1)^2=norm(p_1-p_b)^2+2lambda_1 << p_1-p_b, vec v_1 >> +lambda_1^2 norm(vec v_1)^2# so
#norm(p_1-p_a)^2+2lambda_1 << p_1-p_a, vec v_1 >> =norm(p_1-p_b)^2+2lambda_1 << p_1-p_b, vec v_1 >> # so
#lambda_1^@ = (norm(p_1-p_b)^2-norm(p_1-p_a)^2)/(2<< p_b-p_a, vec v_1 >>)#
The contact point in #L_1# is
#p_c=p_1+lambda_1^@ vec v_1#
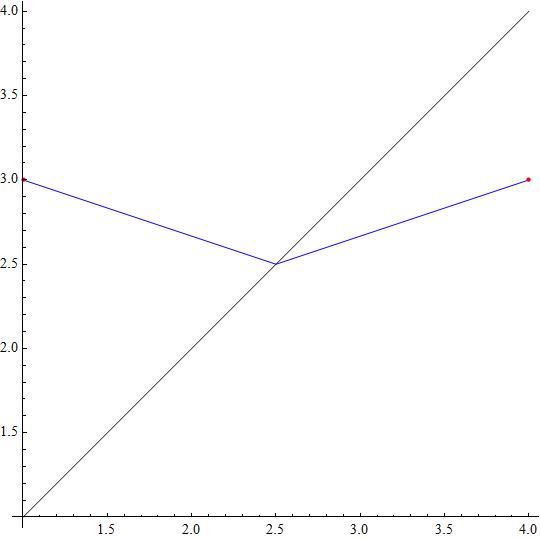
Attached an example with
#p_a = (1,3)#
#p_b = (4,3)#
#p_1 = (1,1)# and
#vec v_1 = (1,1)#
giving
#p_c = (5/2,5/2)#