#((delS)/(delV))_T = alpha/beta#. Prove this relation please?
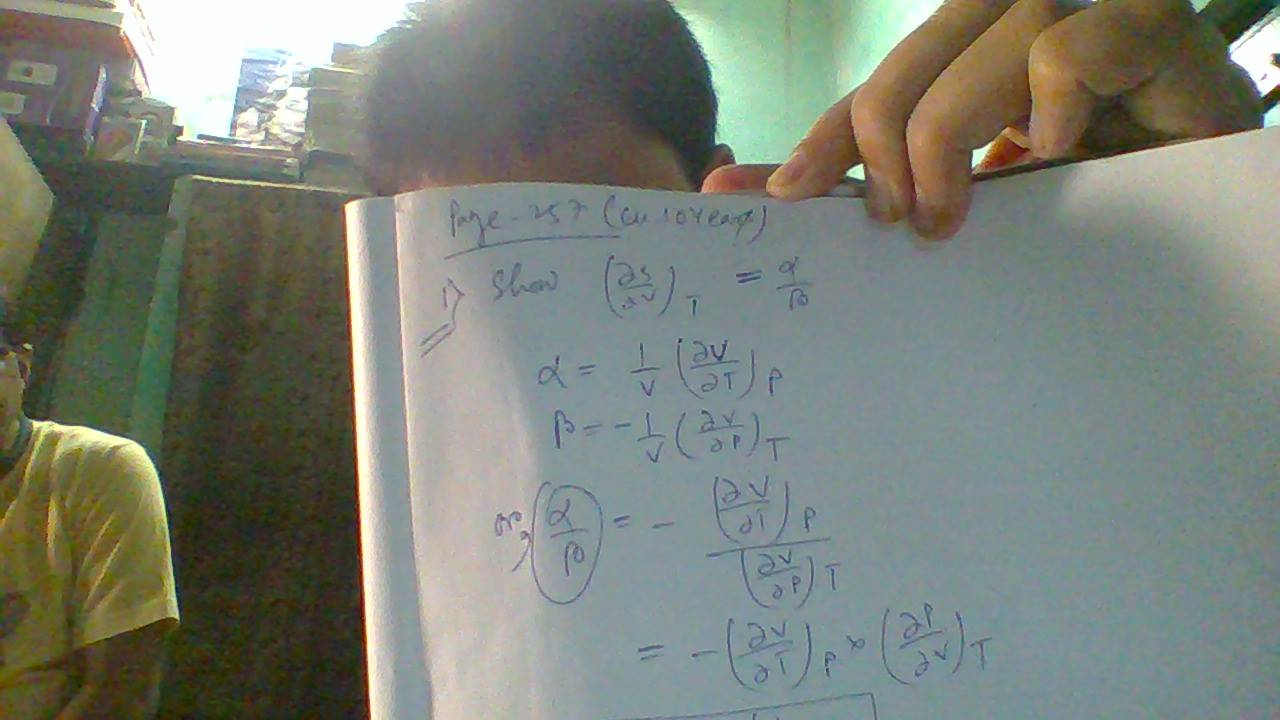
#S = "entropy"#
#V = "volume"#
#alpha = "coefficient of isobaric expansion"#
#beta = "coefficient of isothermal compression"#
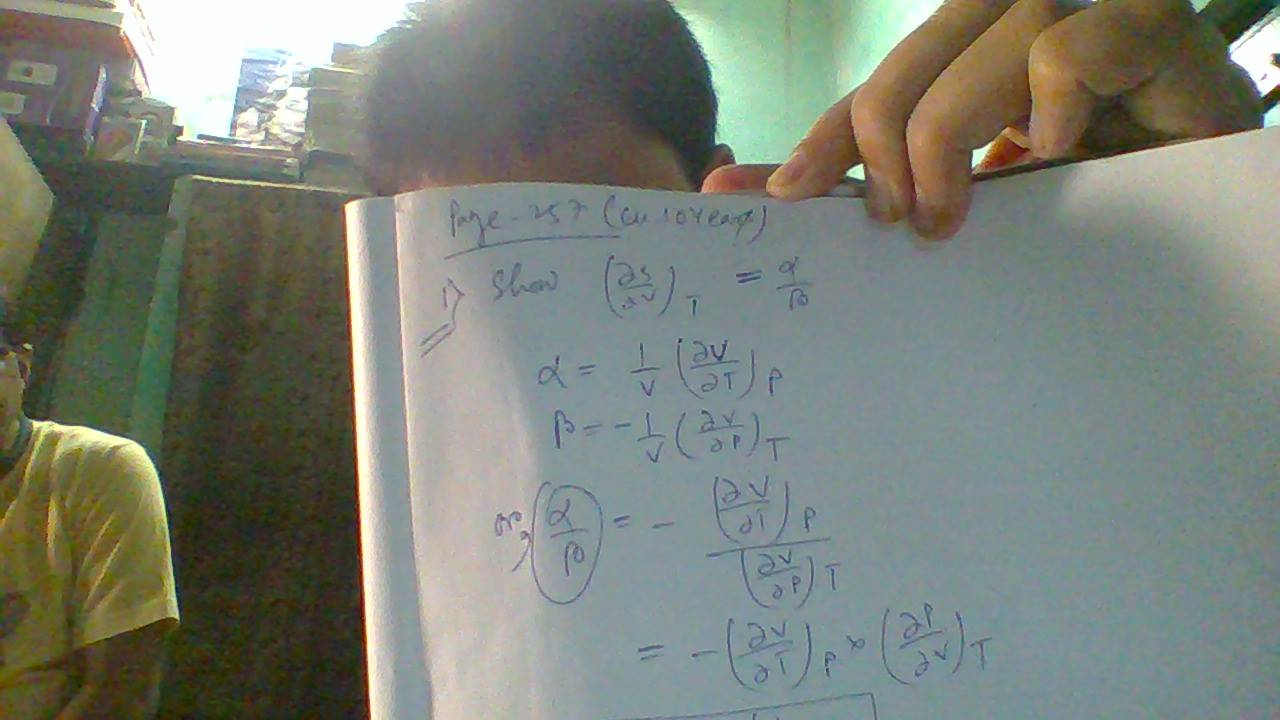
1 Answer
From the definitions of
#alpha = 1/V((delV)/(delT))_P#
#beta = -1/V((delV)/(delP))_T#
Now, since
#dV = ((delV)/(delT))_PdT + ((delV)/(delP))_TdP#
Notice how this contains both
#cancel(((delV)/(delT))_V)^(0) = ((delV)/(delT))_Pcancel(((delT)/(delT))_V)^(1) + ((delV)/(delP))_T((delP)/(delT))_V#
#-((delV)/(delT))_P = ((delV)/(delP))_T((delP)/(delT))_V#
#((delP)/(delT))_V = -[((delV)/(delT))_P]/[((delV)/(delP))_T]#
This looks quite familiar. Considering what
#((delP)/(delT))_V = -[1/V((delV)/(delT))_P]/[1/V((delV)/(delP))_T]#
#= -[alpha]/[-beta] = alpha/beta#
Now we just have to show that
Consider the Helmholtz free energy, the thermodynamic state function that contains the natural variables
#dA = ((delA)/(delT))_VdT + ((delA)/(delV))_TdV#
Just like the Gibbs' free energy, where we had
#bb(dA) = dU - d(TS)#
#= dU - SdT - TdS#
From the first law of thermodynamics for a reversible process in a closed system,
#=> cancel(TdS) - PdV - SdT - cancel(TdS)#
#= bb(-SdT - PdV)#
which gives the Maxwell relation for the Helmholtz free energy. Depending on your professor, you may simply be able to use this relation without deriving it. Compare back to the total derivative to find:
#S = -((delA)/(delT))_V#
#P = -((delA)/(delV))_T#
Since state functions have exact differentials, it follows that the second-order cross-derivatives are equal:
#((del^2A)/(delVdelT))_(V,T) = ((del^2A)/(delTdelV))_(T,V)#
So, let us take the cross-derivatives of the above expressions of
#((delS)/(delV))_T = -((del^2A)/(delVdelT))_(V,T)#
#((delP)/(delT))_V = -((del^2A)/(delTdelV))_(T,V)#
We now see that since the second-order cross-derivatives are equal from the definition of a state function, we've established that
Therefore:
#color(blue)(((delS)/(delV))_T = (alpha)/(beta))#

