Electrolysis: #"Sn"^(2+) "||" "Br"_2# What is the reaction, determine E cell, equilibrium constant and direction of electron flow? Draw cell and label anode and cathode.
1 Answer
Well, consider the data...
#"Br"_2(l) + 2e^(-) -> 2"Br"^(-)(aq)# ,#" "E_(red)^@ = "1.08 V"#
#"Sn"^(2+)(aq) + 2e^(-) -> "Sn"(s)# ,#" "E_(red)^@ = -"0.14 V"#
The spontaneous reaction at
#E_(cell)^@ = E_(red)^@ + E_(o x)^@ > 0# .where
#E_(o x)^@ = -E_(red)^@# is the standard oxidation potential.
The only way for that to occur is to reverse the tin reduction. An electrolysis forces the nonspontaneous reaction, so the reaction is instead::
#color(blue)(E_(cell)^@) = color(red)(-)["1.08 V" + -(-"0.14 V")] = color(blue)(ul(-"1.22 V"))#
and the reaction is:
#-["Br"_2(l) + cancel(2e^(-)) -> 2"Br"^(-)(aq)]# ,#" "E_(red)^@ = color(red)(-)("1.08 V")#
#ul(-["Sn"(s) -> "Sn"^(2+)(aq) + cancel(2e^(-))])# ,#" "E_(o x)^@ = -(color(red)(+)"0.14 V")#
#color(blue)("Sn"^(2+)(aq) + 2"Br"^(-)(aq) -> "Br"_2(l) + "Sn"(s))#
The equilibrium constant can only be calculated when
#cancel(DeltaG)^(0) = DeltaG^@ + RTlncancel(Q)^(K)#
Knowing that, recall that
#-nFE_(cell)^@ = DeltaG^@ = -RTlnK# ,where:
#n# is the mols of electrons transferred per mol of atom.#F = "96485 C/mol e"^(-)# is Faraday's constant.#E_(cell)^@# was just calculated.#DeltaG# is the change in Gibbs' free energy and#@# indicates standard conditions of#"1 bar"# and#25^@ "C"# .- The universal gas constant
#R = "8.314472 V"cdot"C/mol"cdot"K"# and the temperature#T# in#"K"# are well-known from the ideal gas law.
Therefore, the equilibrium constant is:
#color(blue)(K) = "exp"[-(DeltaG^@)/(RT)]#
#= "exp"[(nFE_(cell)^@)/(RT)]#
#= "exp"[((2 cancel("mol e"^(-)))/(cancel("1 mol Sn"^(2+))) cdot (96485 cancel"C")/cancel("mol e"^(-)) cdot -1.22 cancel"V")/(8.314472 cancel"V"cdotcancel"C""/"cancel"mol"cdotcancel"K" cdot 298.15 cancel"K")]#
#=# #color(blue)ul(5.70 xx 10^(-42))#
As it stands, the reaction is clearly nonspontaneous, and it is intended to form
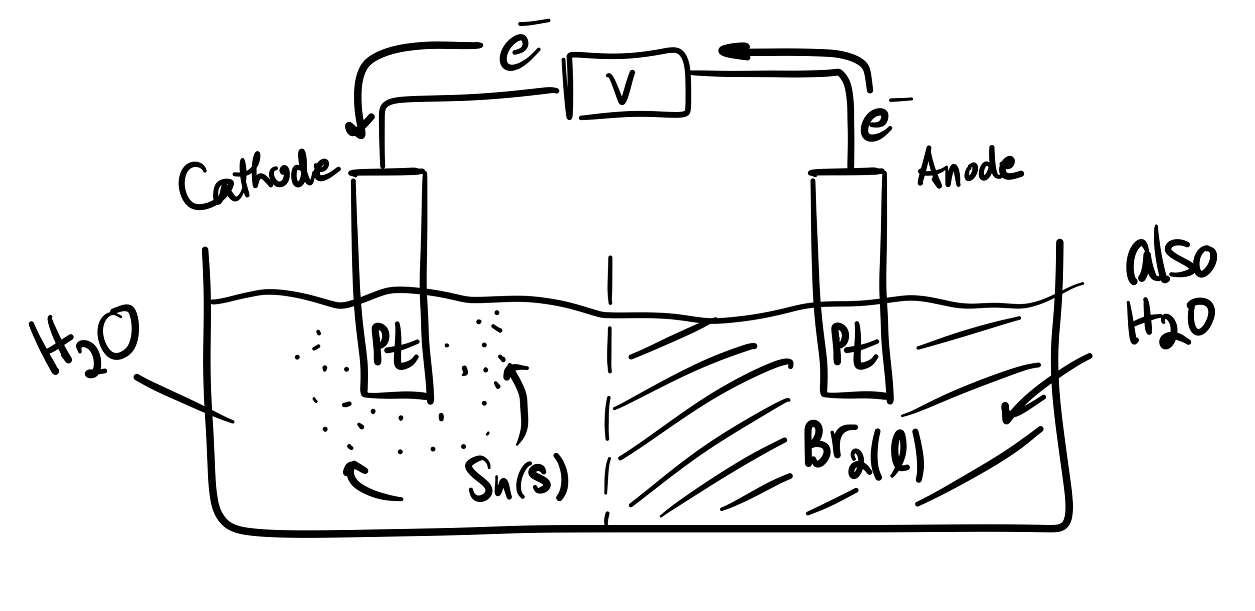
Just like galvanic cells, in electrolytic cells oxidation occurs at the anode and vice versa. However, the electrons instead are forced to flow the nonspontaneous direction. Thus,

