Evaluate the definite integral.?
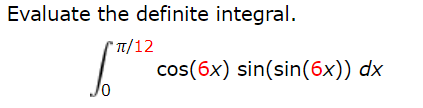
3 Answers
May 28, 2018
Explanation:
Sunstituting
May 28, 2018
I tried this:
Explanation:
Have a look:
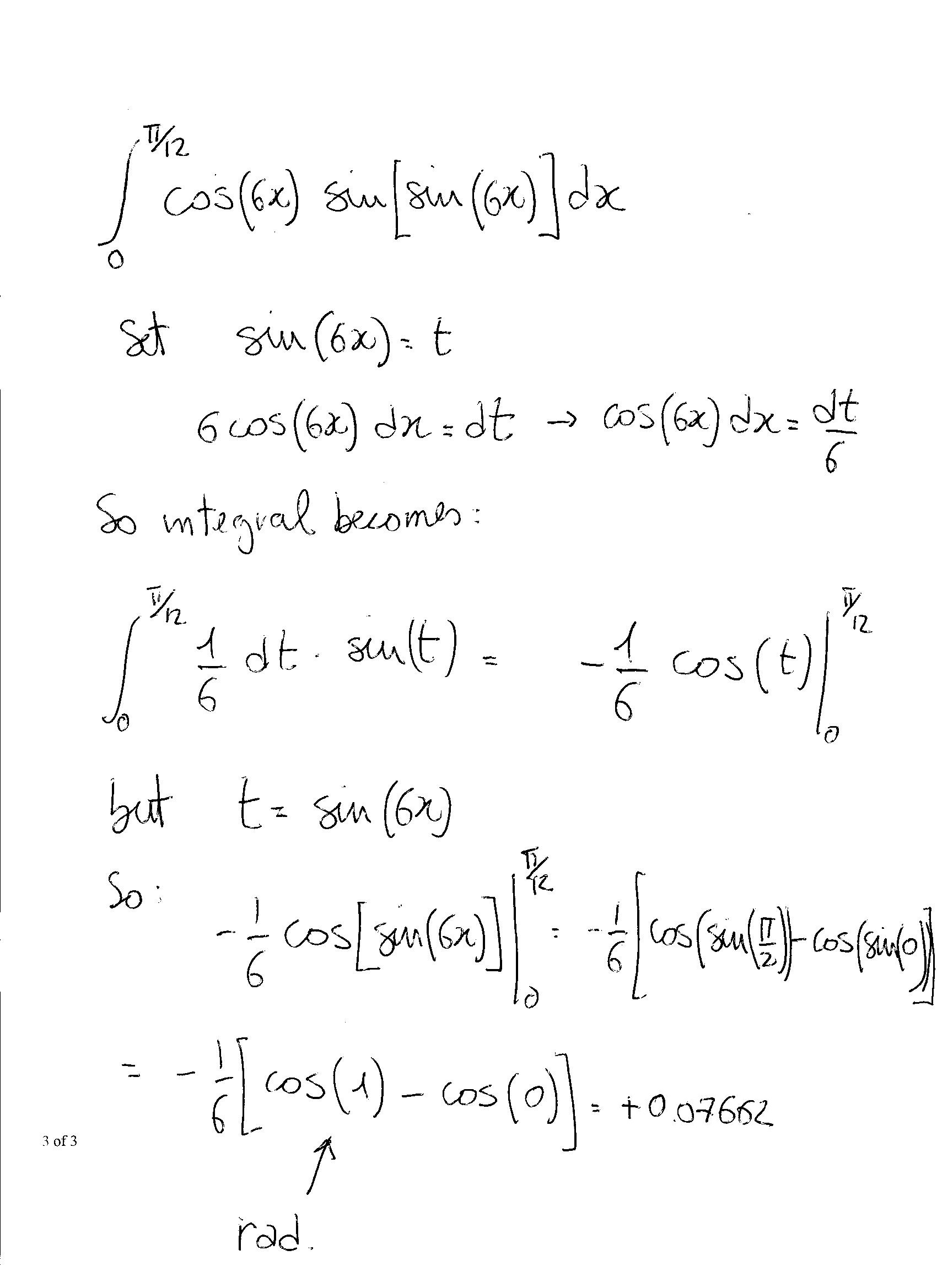
May 28, 2018
Explanation:
Suppose that,
Subst.
Also, when
when


