How is static equilibrium formed?
1 Answer
When the sum of all forces is
A classic example is a man standing on a ladder propped up against a wall.
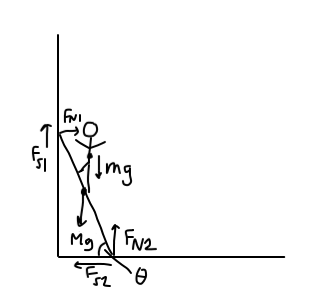
where
#m# is the mass of the man,#M# is the mass of the ladder,#g# is the gravitational constant,#F_s# is the static friction force,#F_N# is the normal force, and#theta# is the angle with the horizontal. Ladder length is#L# .
So, you have, with CW torque = positive, and downward and rightward force being positive:
#sum F_x = F_(N1) - F_(s2) = 0#
#sum F_y = (M+m)g - F_(N2) - F_(s1) = 0#
#sum tau_x = tau_(F_(N1)) + tau_(F_(s2)) = 0#
#sum tau_y = tau_(F_(s1)) - tau_(F_(N2)) - tau_(mg) - tau_(Mg) = 0#
CHALLENGE: If you only knew

