f is a function on RR where f(x)=|x^2-2|, How do you find f^-1(x)?
2 Answers
Look below
Explanation:
first, we have a detail that the function
the function is
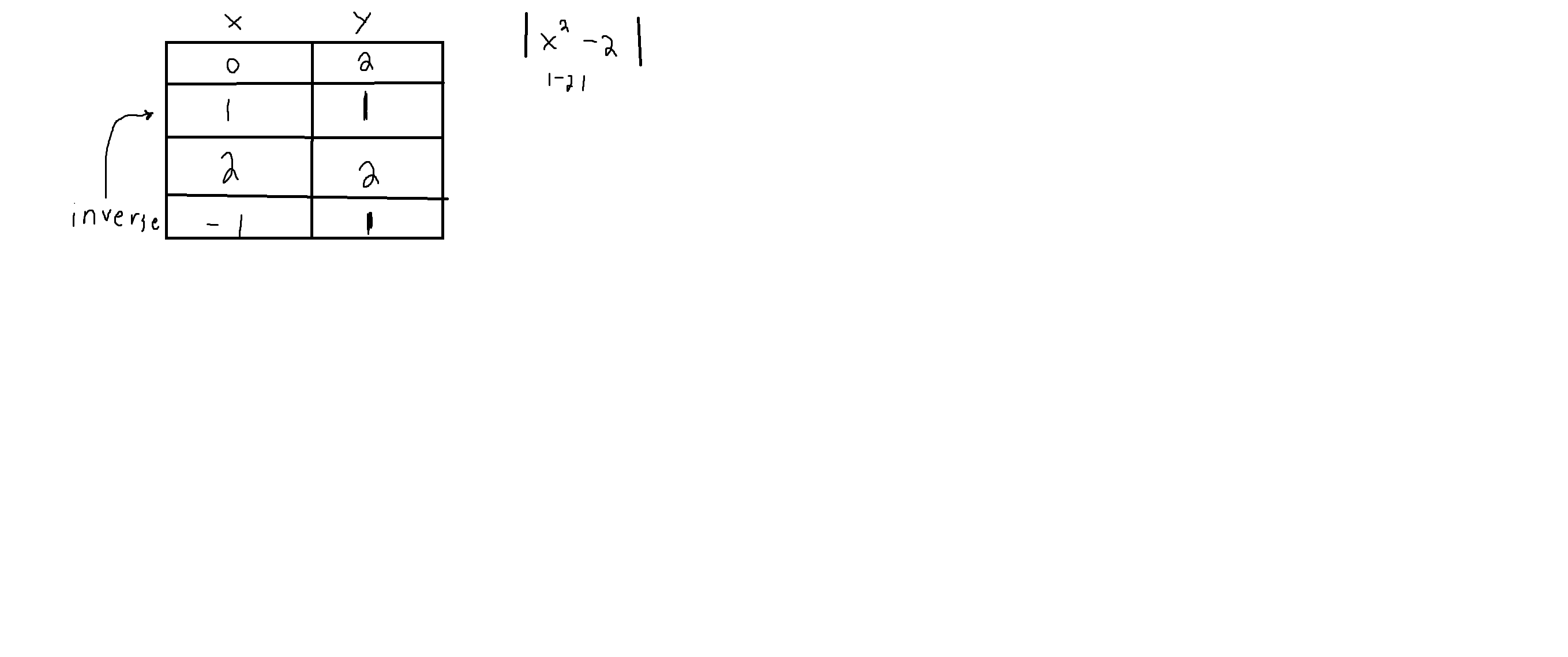 Paint
Paint
now graph the points,
graph{\abs{x^2-2}[-10, 10, -5, 5]}
now, the inverse of an absolute value function is basically the same function, which is
desmos.com
Explanation:
Let's turn
Now, we see that
Similarly, we see that
Therefore, we have:
Let's graph the two parabolas. When we do, we get:
desmos.com
Now, the blue parabola applies when
Therefore, we have(focus on the red graph):
desmos.com
Now, to find its inverse, we have to reflect the red graph over the line
Let's try this mathematically.
Our piece-wise function was:
Let's find the inverse function for each situation.
Now, remember that
Therefore, we can now find the inverse functions.
=>
=>
Similarly,
=>
=>
=>
We now graph these two sideways parabolas:
desmos.com
When
When
We therefore have:
desmos.com
Just note that


