Fill The ICE table, calculate the concentration of each gas, write Kc expression..?
1 Answer
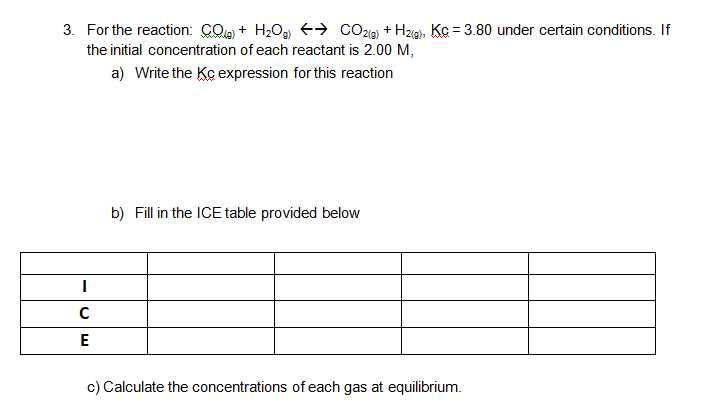
#K_c = (["CO"(g)] * ["H"_2"O" (g)])/(["CO"_2(g)] * ["H"_2(g)]# #c("CO") = c("H"_2"O")~~ 1.356 color(white)(l) "mol"# #c("CO"_2) = c("H"_2)~~ 2.644 color(white)(l) "mol"#
Explanation:
The equilibrium constant is the ratio of the product of the concentration of products (
#color(white)(ll)# #"CO"(g) + "H"_2"O"(g) rightleftharpoons "CO"_2(g) + "H"_2(g)#
I#color(white)(l) 2.00 color(white)(l(g) +) 2.00 color(white)(l_2(g) rightleftharpoons) 2.00 color(white)(g")" +)2.00#
C#-x color(white)(l(g) +) -x color(white)(l(g) rightleftharpoons ) +x color(white)(g")" +) +x#
E#2.00 - x color(white)(lll) 2.00 - x color(white)(rightleftharpoons) 2.00 + x color(white)(l) 2.00 + x#
#((2.00 + x)^2)/((2.00 - x)^2) = K_c = 3.80#
To calculate equilibrium concentrations, substitute
#c("CO") = 2 - x ~~ 1.356 color(white)(l) "M"# -
#c("H"_2"O") = 2 - x~~ 1.356 color(white)(l) "M"# -
#c("CO"_2) = 2 + x ~~ 2.644 color(white)(l) "M"# #c("H"_2) = 2 + x ~~ 2.644 color(white)(l) "M"#

