Question

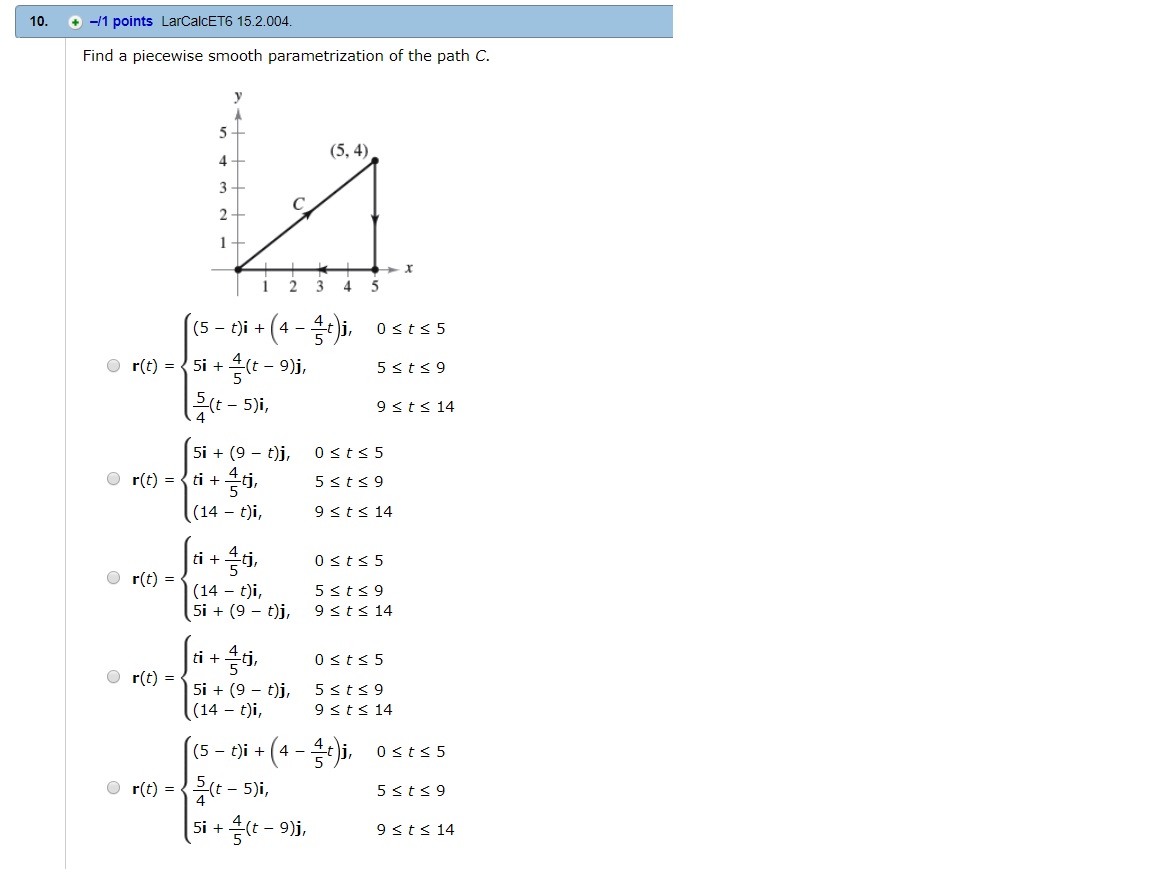
Find a piecewise smooth parametrization of the path C?

Answer 1

The fourth option is the correct one.

Explanation:

Note that all of the suggested options are linear in `t`, so it suffices to check the endpoints in each interval.

First option

Putting `t=0` and `t=5` into the first expression, we get:

`(5-(color(blue)(0)))hat(i)+(4-4/5(color(blue)(0)))hat(j) = (5, 4)`

`(5-(color(blue)(5)))hat(i)+(4-4/5(color(blue)(5)))hat(j) = (0, 0)`

So this traverses the segment between `(0, 0)` and `(5, 4)` backwards. So we can reject the first option.

Second option

Putting `t=0` into the first expression, we get:

`5hat(i)+(9-(color(blue)(0)))hat(j) = (5, 9)`

This point is not on the curve, so we can reject the second option.

Third option

The first expression is fine, but putting `t=5` into the second expression gives us the point `(9, 0)` which is not on the curve.

Fourth option

This one works:

• Evaluating the endpoints of the first expression gives `(0, 0)` and `(5, 4)`

• Evaluating the endpoints of the second expression gives `(5, 4)` and `(5, 0)`

• Evaluating the endpoints of the third expression gives `(5, 0)` and `(0, 0)`

So this parametrisation traverses the curve as required.