Find all value of α in [0°, 360°) that will satisfy this equation? 2sinα=-√3
2 Answers
Apr 8, 2018
Explanation:
Isolate the sine.
Consider where, in the interval
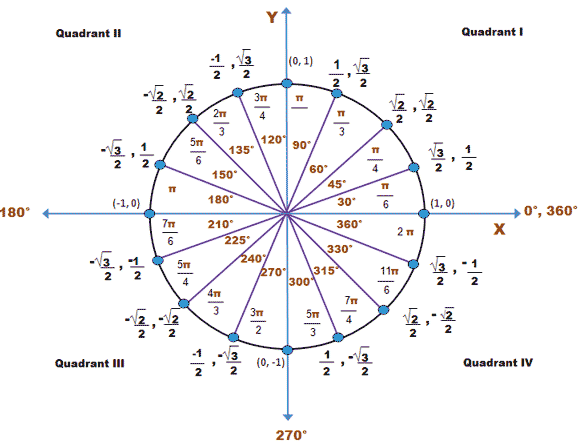
So, from the unit circle itself, we get
Apr 8, 2018
Explanation:
Divide by 2:
Look at the unit circle to see when y is equal to
graph{2sinx+sqrt3 [-10, 10, -5, 5]}


