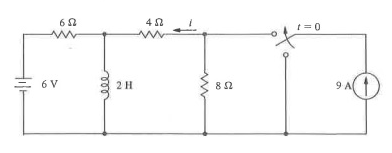
At #t<0# the system is in steady state. So, the inductor behaves like a short and hence no current flows through the #4\ Omega# resistance. So, the initial condition is
#i = 0# at #t = 0#
For #t>0# the current through the #8\ Omega# resistance is #9\ "A"-i#, and so the voltage across it is
#8\ Omega times (9\ "A"-i) = 72\ "V" - 8\ Omega times i#
If the current through the inductance is #i^'# then that through the #6\ Omega# resistance is #i-i^'# and so, we have
# 72\ "V" - 8\ Omega times i = 4\ Omega times i +6\Omega times (i-i^') + 6\ "V"#
and hence
#18i-6i^' = 66\ "A" implies i^' = 3i-11\ "A" implies {di^'}/{dt} = 3{di}/{dt}#
Again, by using the fact that the voltage drop across the inductor is given by #2\ "H" times {di^'}/dt# we get
# 72\ "V" - 8\ Omega times i = 4\ Omega times i +2\ "H" times {di^'}/dt#
So, the differential equation for #i(t)# finally takes the form
#{di}/dt + lambda i= \Lambda#
where #\lambda = 2\ "s"^-1# and #\Lambda = 12\ "A"\ "s"^-1#
This differential equation can finally be cast in the form
#d/dt (Lambda/lambda-i) = -lambda(Lambda/lambda-i)#
which is easy to integrate to give
#ln (i_oo-i) = -lambda t+C#
where #i_oo = Lambda/lambda = 6\ "A"#. From the initial condition, we get
#C = ln (i_oo)#
so that
#1-i/i_oo = e^{-lambda t}# and thus finally
#i(t) = i_oo(1-e^{-lambda t})#