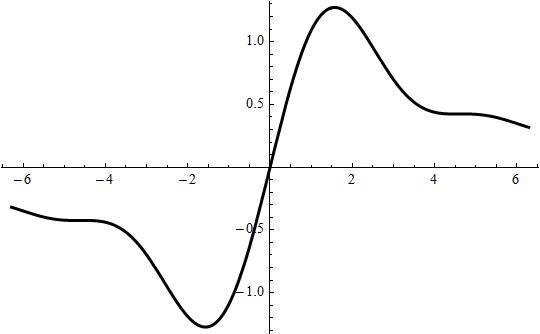
Find maxima of the following expression using calculus (2x-sin2x)/x^2 ?
1 Answer
Explanation:
Given
the stationary points are determined solving for
or
with solutions
Here
Now testing in the range
we will obtain
and for
there are infinite minima and maxima for
Note:
We have obviate the limit determination for
For qualification justification see
https://socratic.org/questions/if-f-x-x-8-9-x-4-7-x-3-7-what-are-the-local-minima-and-maxima-of-f-x#300548
Attached the plot of