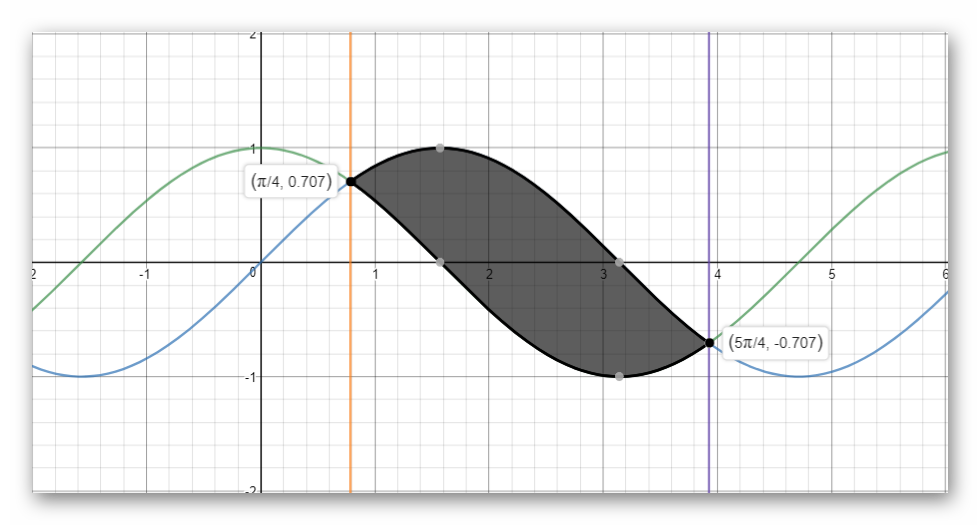
Find the area bounded by f(x)=sinx and g(x)=cosx from x=pi/4 to x=((5pi)/4.. Make an accurate sketch of the graphs on the axis below?
Find the area bounded by f(x)=sinx and g(x)=cosx from x=pi/4 to x=((5pi)/4) . Make an accurate sketch of the graphs on the axis below.

Find the area bounded by

1 Answer
May 30, 2018
Explanation:
The Area due to
The interval of our integral
now let set up the integral:
show the wanted area below(shaded):
 James
James

