Find the area bounded by the curve y=e^(x/3) , the tangent line which is y=1/3 e^(3)x - 2e^3 and the x-axis?

Do I need integration by part to do this?

1 Answer
Ananda Dasgupta
Jun 4, 2018

#3/2e^3-3#

Explanation:

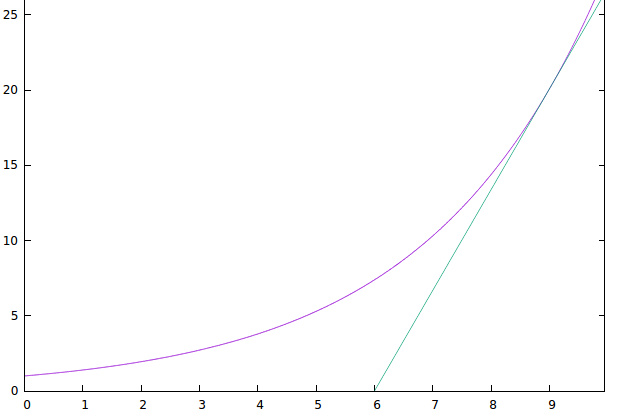
enter image source here

The straight line #y=1/2e^{3}x-2e^3# is tangent to #y=e^{x/3}# at the point #(9,e^3)#. It is also easy to see that it cuts the #X# axis at #(6,0)#

The area under the curve #y=e^{x/3}# from #x=0# to #x = 9# is given by

#int_0^9 e^{x/3}dx = [3 e^{x/3}]_0^9 = 3e^3-3#

The area that we are looking for is the difference between the area under the curve #y=e^{x/3}# from #x=0# to #x = 9# and the area of the triangle with vertices at #(6,0)#, #(9,0)# and #(9,e^3#). The area of the triangle is #1/2 times 3 times e^3 = 3/2e^3#

Thus the area that we need is

#3e^3-3-3/2e^3 = 3/2e^3-3#

Related questions
Impact of this question
1793 views around the world
You can reuse this answer
Creative Commons License