The reason why I am making #x# the subject of both equations is to make it easier for me to integrate a parabola ( #y^2-4x+4=0# ).
Equation 1: #y^2-4x+4=0#
Make #x# the subject,
#4x=y^2+4#
#x=y^2/4+1#
Equation 2: #x-y=4#
Make #x# the subject again,
#x=y+4#
#ulcolor(white)((xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx)#
Apply simultaneous equations,
#y^2/4+1=y+4#
Multiply both sides by #4#,
#y^2+4=4y+16#
Move all terms to one side,
#y^2-4y-12=0#
Factorise,
#(y-6)(y+2)=0#
Solve,
#y=6 or -2#
When #y=6#,
#x=10#
When #y=-2#
#x=2#
Hence, the intercepts of the equations are,
#(10,6) or (2,-2)#
#ulcolor(white)((xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx)#
To find the area enclosed, form an integral
#int_-2^6" "(y+4)-(y^2/4+1)" "dy#
Expand parenthesis and simplify,
#int_-2^6" "-y^2/4+y+3" "dy#
Integrate,
#[-y^3/12+y^2/2+3y]_-2^6#
Compute limits,
#[-(6)^3/12+(6)^2/2+3(6)]-[-(-2)^3/12+(-2)^2/2+3(-2)]#
Solve,
#63/4~~21.333 units^2#
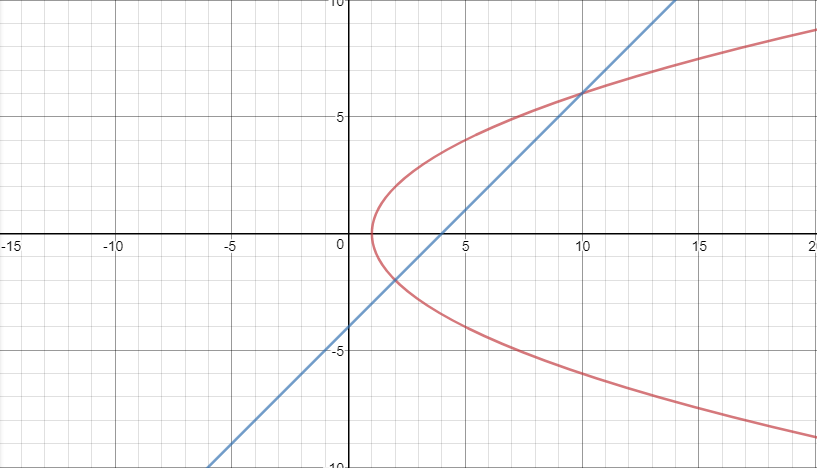
For reference, here is a graph: