.
Let's draw a picture of this #9#-gon:
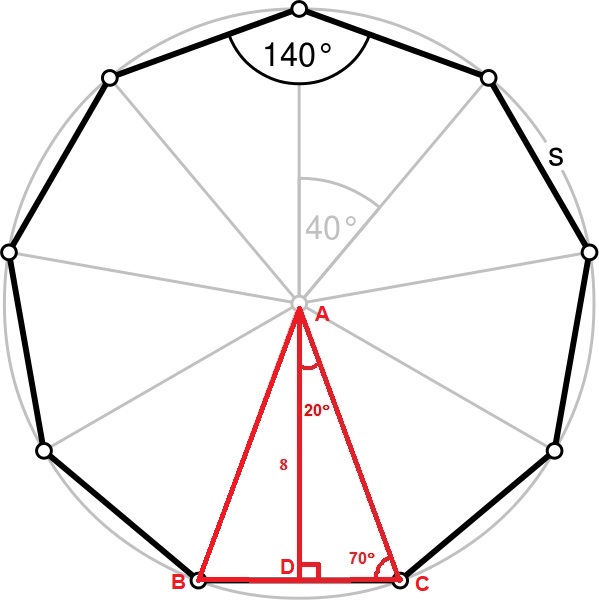
The area of a regular #9#-gon is divided into #9# congruent (equal) isosceles triangles. I have shown one of them in red.
The angle #/_BAC=360^@/9=40^@#
Because triangle #DeltaABC# is isosceles, its altitude #AD# which is the apothem of the #9#-gon divides angle #/_BAC# into two equal angles of #20^@#:
#/_DAC=20^@#
#tan/_DAC=("Opposite")/("Adjecent")=(DC)/(AD)#
#tan20^@=(DC)/8#
#0.36=(DC)/8#
#DC=(0.36)(8)=2.88#
In the isosceles triangle #DeltaABC#, the altitude divides the base into two equal halves. Therefore,
#BC=2DC=(2)(2.88)=5.76#
The area of #DeltaABC# is:
#A_(DeltaABC)=BC(AD)/2=(5.76)*(8/2)=23.04#
The area of the #9#-gon is nine times the area of #DeltaABC#:
#A_(9-gon)=9(23.04)=207.36#


