We know that ,
"If "P(x_1,y_1) ,Q(x_2,y_2),R(x_3,y_3) are the vertices of
triangle PQR, then area of triangle:
Delta=1/2||D||, where , D=|(x_1,y_1,1) ,(x_2,y_2,1),(x_3,y_3,1)|........................(1)
Plot the graph as shown below.
Consider the points in order, as shown in the graph.
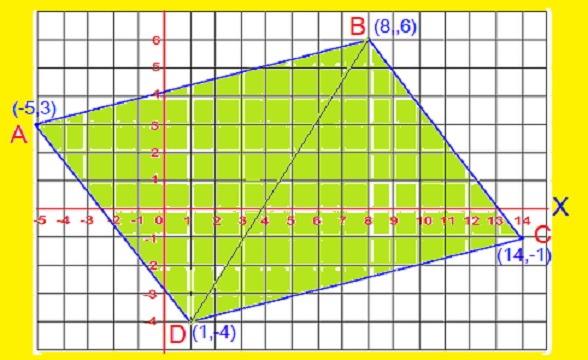
Let A(-5,3) ,B(8,6) ,C(14,-1) and D(1,-4) be the vertices of Parallelogram ABCD.
We know that ,
"Each diagonal of a parallelogram separates parallelogram"
"into congruent triangles."
Let bar(BD) be the diagonal.
So, triangleABD~=triangleBDC
:. "Area of parallelogram "ABCD=2xx "area of"triangleABD "
Using (1),we get
Delta=1/2||D|| ,where, D=|(-5,3,1),(8,6,1),(1,-4,1)|
Expanding we get
:.D=-5(6+4)-3(8-1)+1(-32-6)
:.D=-50-21-38=-109
:.Delta=1/2||-109||=109/2
:.Delta=54.5
:. "Area of parallelogram "ABCD=2xx "area of"triangleABD "
:. "Area of parallelogram "ABCD=2xx(109/2)=109
:. "Area of parallelogram "ABCD=109 " sq. units"


