Find the area of the region enclosed by y=ln(x) ,the x-axis,the y-axis and y=1 ? (a) dx select (b) dy select
Please help me
Please help me
2 Answers
Explanation:
I have the graphs of the functions and lines here:
We want the area of the green region.
We can think of the situation like this:
Now, let's find the intercept and the intersection.
The intercept:
The intersection:
We can now form a rectangle like the following:
The area of the green region is the area of the rectangle minus the area under the curve of
The fundamental theorem of calculus:
Remember that
In case you are wondering how I solved
Explanation:
.
Let's take a look at the graph of this area:
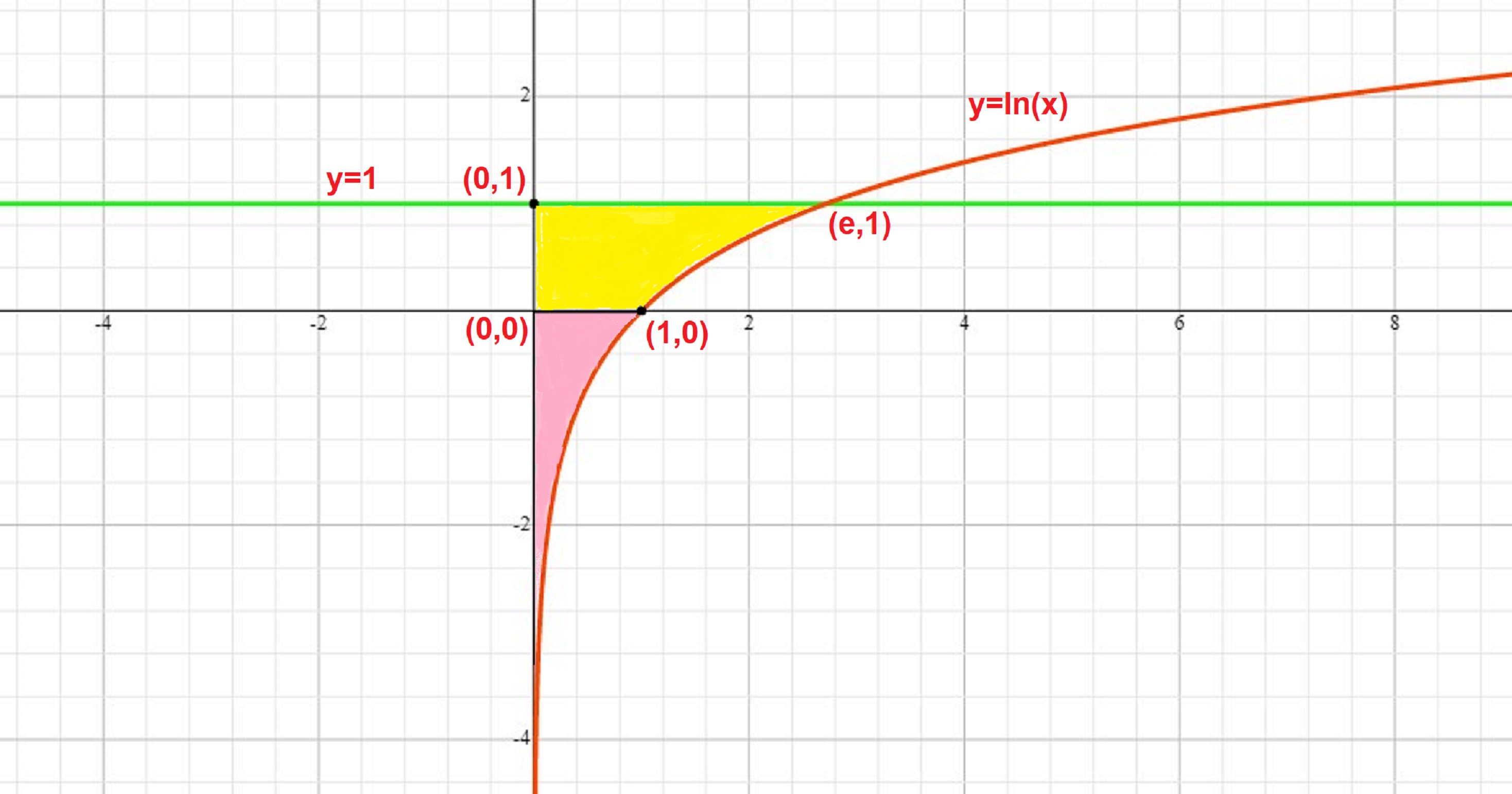
The area described in the problem is shaded in yellow. If we use integration along the
This will give us the combination of the yellow and pink areas.
Then we will set up another integral to calculate the area between the
To calculate the
If we use integration along the
Now, we can use one integral to calculate the area between the


