Question

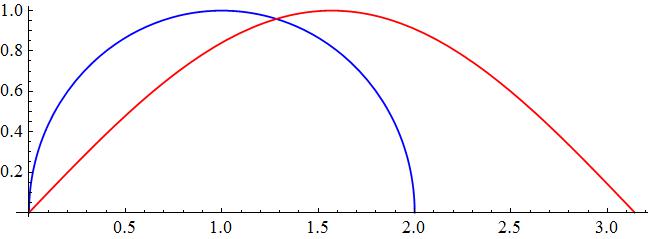
Find the average height of a point on a unit semi-circle?

I know that there are two ways of finding the average height of a point on a unit semi circle. The first method involves adding up the heights of an infinite number of points between 1 and -1 and then divide by the total number of points.
The height of each point is given by the explicit equation of the upper unit semi circle (1-x^2)^1/2
Avg(f)=1/(1-(-1)) (∫(1-x^2)^1/2)=pi/4 from x=-1 to x=1

In the second method, we take the average of the function with respect arc length, this time the average is given by 1/pi ∫sinθdθ from θ=0 to θ=pi. Why is the value of the average different when we changed the variable from x to θ even though we are taking the average of the same quantity, the heights of all the points on the unit semi circle.

~~~~~~~~~~~~~~~~~

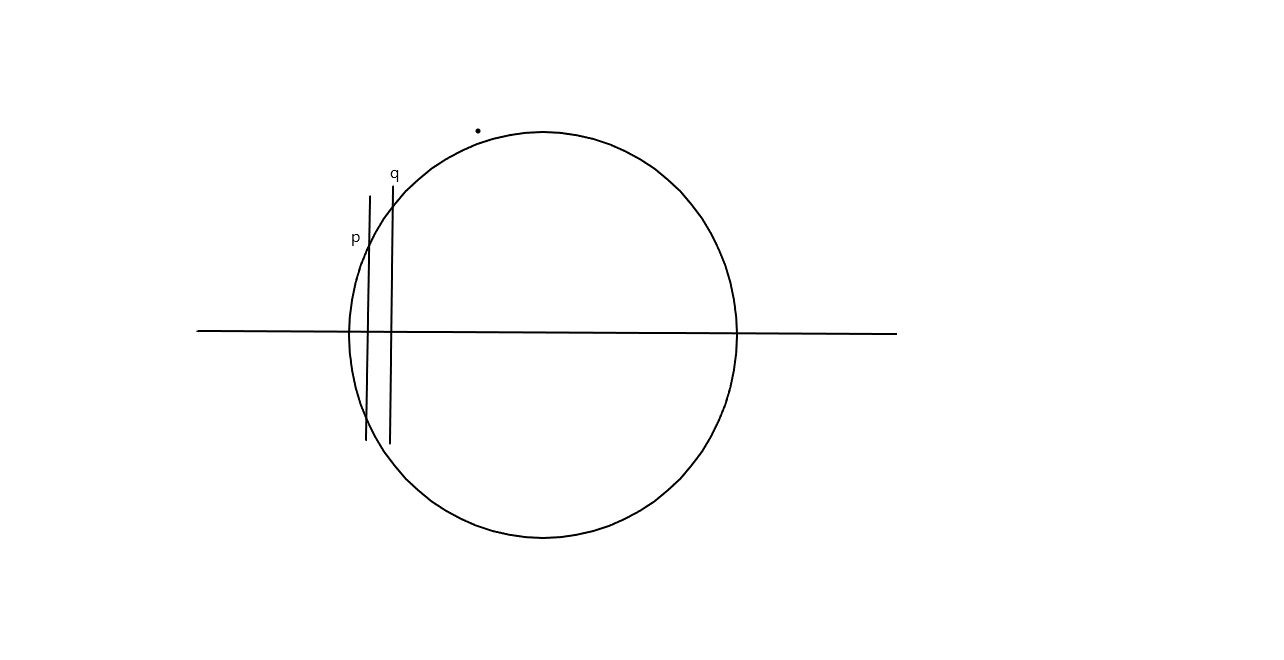
That's what I wanted to say in a picture

Answer 1

No differences at all!

In Cartesian coordinates

`bar y = 1/(b-a)int_(a)^by(x) dx`

Here `y(x)` is the upper semi-circle so

`y(x) = sqrt(r^2-x^2)` and

`bar y = 1/(2r)int_(-r)^r sqrt(r^2-x^2) dx = pi/4` assuming `r = 1`

and in polar coordinates knowing that

`{(x = r cos theta),(y = r sin theta):}`

with `r = C^(te)` we have

`dx =r sin theta d theta`

so in polar coordinates

`bar y = 1/(2r)int_0^pi r sin theta(r sin theta d theta)` or

`bar y = 1/(2r) r^2int_0^pi sin^2 theta d theta = pi/4` assuming `r = 1`

NOTE:

The error is in considering `bar y = 1/pi int_0^pi sin theta d theta`

The sign consideration in `dx = r sin theta d theta` as positive, is left as an exercise.

Answer 2

Please see below. Warning -- long answer.

Explanation:

The average value -- the ordinary average value with respect to `x` over interval `[a,b]` is found by:

Start with a finite average as an approximation
Cut the interval into `n` equal subintervals of length `Delta x = (b-a)/n`.
On each subinterval, use a single value of `x` (which I'll call `x_i`) to find `f(x_i)` as the height throughout the interval.
Sum the values of `f(x_i)` and divide by `n`

`(sum_(i=1)^n f(x_i))/n`

As `nrarroo`, this approximation gets better and better.

And the limit as `nrarroo` is the average value of `f` on `[a,b]`

`Deltax = (b-a)/n` so `n = (b-a)/(Deltax)` and

`lim_(nrarroo)((sum_(i=1)^n f(x_i))/n) = lim_(nrarroo)(sum_(i=1)^n f(x_i)Delta x)/(b-a)`

`= 1/(b-a) lim_(nrarroo)(sum_(i=1)^n f(x_i)Delta x)`

`= 1/(b-a) int_a^b f(x) dx`

For the upper unit semicircle , we have:

`[a,b] = [-1,1]` so that `Delta x = 2/n`

Using the right enpoint of each subinterval as our representative point, we have `x_i = -1+(2i)/n` and the heoght at that point is `sqrt(1-x_i^2)`

So the average height is

`1/2lim_(nrarroo)sum_(i=1)^nsqrt(1-x_i^2)Delta x = 1/2lim_(nrarroo)sum_(i=1)^nsqrt(1-x_i^2)(2/n)`

`= 1/2int_1^1sqrt(1-x^2)dx`

The average with respect to arc length cuts the curve (not an interval on the `x` axis) into `n` equal pieces and again uses a representative value to approximate the average, the takes the limit as the number of subarcs of the curve increases without bound (not subintervals of the domain interval).

I'd like to use `t` for arc length.

For the upper unit semicircle , we have `t in [0,pi]` we cut the semicircle into `n` equal arcs, each of length `Delta t = pi/n`.
For each subarc, I'll use the greatest value of `t`, which is `t_i = 0+(ipi/n) = (ipi)/n`
The height of the point on the semicircle is `sint_i`. So the average value w.r.t. arc length is

`lim_(nrarroo)sum_(i=1)^n ((sint_i)/n)` `" "` where `n = pi/(Delta t)`

So the average height w.r.t arc length is

`1/pi lim_(nrarroo)sum_(i=1)^n ((sint_i)Delta t) = 1/pi lim_(nrarroo)sum_(i=1)^n (sint_i)(pi/n)`

I don't see a reason to expect equality between

`1/2lim_(nrarroo)sum_(i=1)^nsqrt(1-(-1+(2i)/n)^2)(2/n)` and

`1/pi lim_(nrarroo)sum_(i=1)^n (sin((ipi)/n)(pi/n))`

Further discussion
Arcs of equal length on the semicircle do not correspond to arcs of equal length on the `x` axis.

For example the arcs of length `pi/6` from

`t=0` to `t = pi/6` corresponds to an interval on the `x` axis of length `cos0-cos(pi/6) = (2-sqrt3)/2 ~~ 0.134`

`t=pi/6` to `t = pi/3` corresponds to an interval on the `x` axis of length `cos(pi/6)-cos(pi/3) = (sqrt3-1)/2 ~~ 0.366`

`t=pi/6` to `t = pi/2` corresponds to an interval on the `x` axis of length `cos(pi/3)-cos(pi/2) = (1-0)/2 = 0.5`

As the document I linked says "Points on the semicircle with lower height 'count for more' in the computation with respect to arc length".

Quoted from: https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/unit-3-the-definite-integral-and-its-applications/part-c-average-value-probability-and-numerical-integration/session-60-integrals-and-averages/MIT18_01SCF10_Ses60c.pdf

Answer 3

See below.

Explanation:

Let `s` be the arc length for an unit semi-circle. The sought
average is

`1/(Delta s)int_(s=0)^(s=Delta s)y(s)ds`

Here `y(s) = y(r theta) = r sin theta` and `ds = r d theta` but `r = 1` then

`1/(Delta theta) int_(theta = 0)^(theta = Delta theta) sin theta d theta = -1/(Delta theta)[cos theta ]_0^(Delta theta) = (1-cos(Delta theta))/(Delta theta)`

For `Delta theta = pi` we have

`1/pi int_(theta = 0)^(theta = pi) sin theta d theta =2/pi`

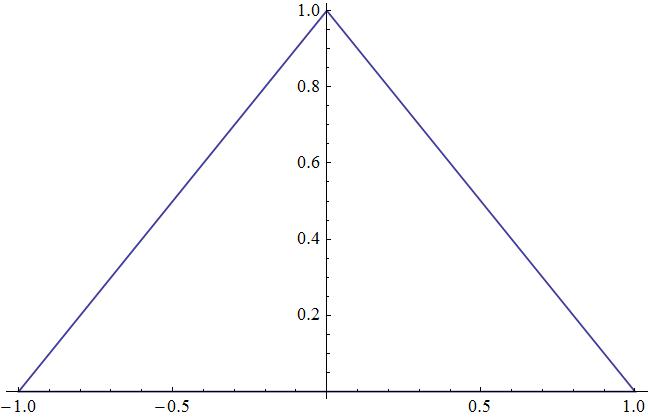
Suppose now that we need

`bar y = 1/(Delta x)int_(x=0)^(x= Deltax) y(x) dx` with `Delta x = 1-(-1) = 2`

then

`bar y = 1/2 xx 1 = 1/2`

and now

`bar y = 1/(Delta s) int_(s=0)^(s = Delta s)y(s)ds`

In this case `s = sqrt2 x` for `x in [-1,0]` and `y(s) = s/sqrt2` The problem has one symmetry and then considering `Delta s = 2 sqrt 2` we have

`bar y =1/(2 sqrt2)(int_(x = 0)^(x=sqrt2)x/sqrt2 dx+int_(x =0)^(x=sqrt2)x/sqrt2 dx ) = 1/(2(sqrt2)^2)[ x^2]_0^sqrt2 = 1/2`

As can we observe, in the linear case the result is the same.

Attached a plot with the comparison between `y(x)` in blue and `y(s)` in red for the semi-circle case. It is notorious that the measures are distinct!