Question

Find the average rate of change of the function between the given points? `f(x)=3sqrt(x-5)` `x=6, x=10`

Answer 1

See below.

Explanation:

The average rate of change over an interval `[a,b]`, is given by:

`(f(b)-f(a))/(b-a)`

You can see that this is the same method as finding the gradient of a line, i.e.

`(y_2-y_1)/(x_2-x_1)`

In the diagram below, you can see the points at `x=6` and `x=10` are joined by a straight line. This is known as a secant line. The average rate of change is the gradient of this secant line.

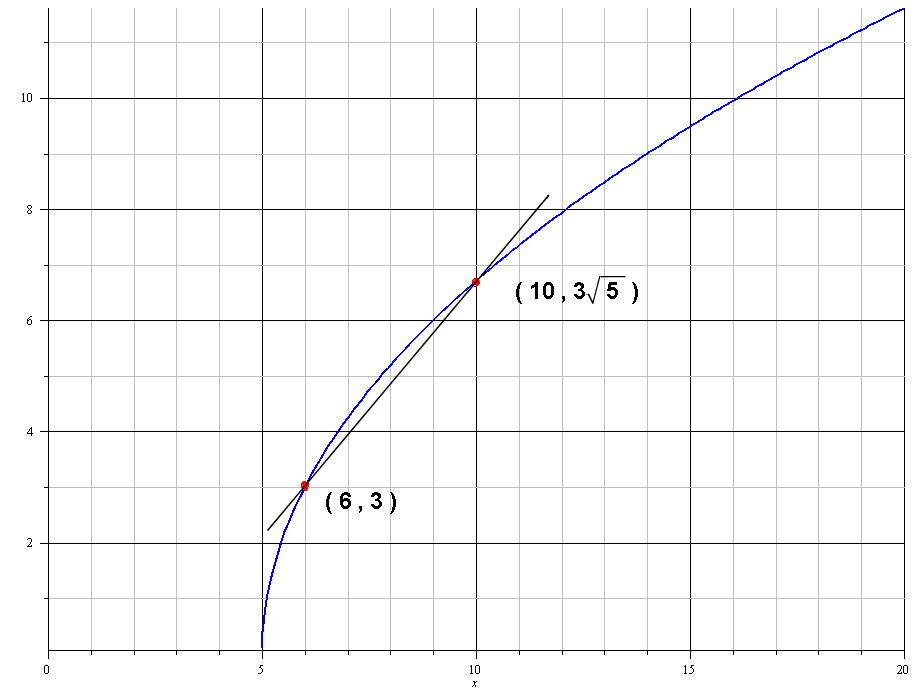
To our example:

`f(x)=3sqrt(x-5)`

`((3sqrt(b-5))-(3sqrt(a-5)))/(b-a)`

We plug in the values for a and b

`:.`

`((3sqrt(10-5))-(3sqrt(6-5)))/(10-6)=((3sqrt(5))-(3sqrt(1)))/(4)=(3sqrt(5)-3)/4`

`color(blue)("Average Rate of Change"=(3sqrt(5)-3)/4)`

Note

In the above we took the `sqrt(1)` as `1` and ignored `-1` which is also a root of `1`. We can justify this by the fact that:

It is generally accepted that when we express a function:

`f(x)=sqrt(x)color(white)(88)`We are implying the positive root.

We can not have both positive and negative roots at the same time. This by definition would not be a function.