Question

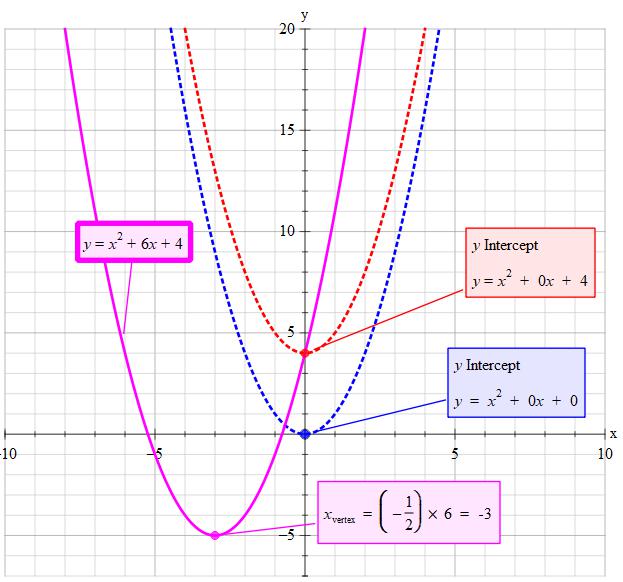
Find the axis of symmetry, Vertex and Y- Intercept and sketch the Parabola and label all parts? `y= x^2 + 6x +4`

i dont understand any of it

Answer 1

Talking about what the equation is saying.

Explanation:

The general shape of a quadratic graph is called a parabola. It is just a name but one worth remembering. On the whole we have the generic shapes `nn and uu`. If you ever do higher maths you will come across `sub and sup` as well.

`y=ax^2 ->` where a is positive we have the general shape `uu`
`y=ax^2->` where a is negative we have the general shape `nn`

If `a` is some where between but not including `-1" to "+1`
then the shape `nn or uu` is widened

If `a` is greater than 1 or less than -1 the general shape of `nn or uu` is narrowed.

Note that `y=x^2` is of form `y=ax+0x+0`

This part in the given question is `y=1x^2+...." so "a=1`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

What happens if we add the constant 4

`y=x^2+4`

The 4 is the value on the y-axis through which the graph passes. It is the y-intercept. So it lifts `y=x^2` upwards by 4.
No matter how you change the equation, if the constant is 4 then the graph will always pass through that point on the y-axis.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
What happens if we add `6x`

This particular part defines the `x` value of the vertex

`x_("vertex")=(-1/2)xx6 = -3`

By substitution you can determine the value of `y_("vertex")`

There are other ways of determining the vertex.
Completing the square or half way between where the graph crosses the x-axis.

`color(brown)("This will do for now! You will learn more as you go on.")`