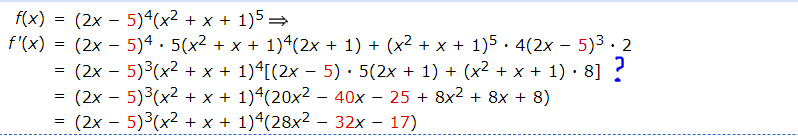# "Yes, this is a simplification technique that may be described as" #
# "factoring out the" \ lowest \ "powers of common exponentiated" #
# "factors. It is very powerful, and makes some simplifications a" #
# "lot easier and faster, and can get you to the end result very" #
# "directly." #
# "[It works for any exponents -- positive, negative, fractional, any.]" #
# "In the case you have, at the line prior to line 3, you had:" #
# \qquad f'(x) \ = \ ( 2 x - 5 )^4 \cdot 5 ( x^2 + x + 1 )^4 ( 2 x + 1 ) #
# \qquad \qquad \qquad \qquad \qquad \qquad + ( x^2 + x + 1 )^5 \cdot 4 ( 2 x - 5 )^3 cdot 2. #
# "Maybe to illustrate the technique more easily, let me name" #
# "the common exponentiated factors here:" #
# \qquad \qquad \qquad \qquad \qquad \qquad A = 2 x - 5, \qquad B = x^2 + x + 1. #
# "Now we can rewrite" \ \ f'(x) \ \ "as:" #
# \qquad f'(x) \ = \ ( 2 x - 5 )^4 \cdot 5 ( x^2 + x + 1 )^4 ( 2 x + 1 ) #
# \qquad \qquad \qquad \qquad \qquad \qquad + ( x^2 + x + 1 )^5 \cdot 4 ( 2 x - 5 )^3 cdot 2 #
# \qquad \qquad \qquad \quad = \ A^4 \cdot 5 B^4 ( 2 x + 1 ) + B^5 \cdot 4 A^3 cdot 2 #
# \qquad \qquad \qquad \quad = \ A^4 B^4 \cdot 5 ( 2 x + 1 ) + A^3 B^5 \cdot 4 cdot 2 . #
# "Now factor out the" \ lowest \ "powers of the quantites" \ A, B ":" #
# \qquad f'(x) \ = \ A^4 B^4 \cdot 5 ( 2 x + 1 ) + A^3 B^5 \cdot 4 cdot 2 . #
# \qquad \qquad \qquad \quad = \ A^3 B^4 [ A \cdot 5 ( 2 x + 1 ) + B \cdot 4 cdot 2 ] . #
# "Now let's return" \ \ A, B \ \ "to their original values, as we assigned" #
# "them above:" #
# \qquad f'(x) \ = \ A^4 B^4 \cdot 5 ( 2 x + 1 ) + A^3 B^5 \cdot 4 cdot 2 #
# :. \qquad f'(x) \ = \ ( 2 x - 5 )^3 ( x^2 + x + 1 )^4 [ ( 2 x - 5 ) \cdot 5 ( 2 x + 1 ) #
# \qquad \qquad \qquad \qquad \qquad \qquad \qquad + ( x^2 + x + 1 ) \cdot 4 cdot 2 ] . #
# "(Sorry for the line breaks, system can go no farther !!)" #
# "This is how you go from line (2) to line (3), in the example you" #
# "provided. I think this is what you wanted explained. But just" #
# "to be sure, let me continue, and finish the problem as you gave" #
# "it." #
# "So, continuing:" #
# :. \qquad f'(x) \ = \ ( 2 x - 5 )^3 ( x^2 + x + 1 )^4 [ ( 2 x - 5 ) \cdot 5 ( 2 x + 1 ) #
# \qquad \qquad \qquad \qquad \qquad \qquad \qquad + ( x^2 + x + 1 ) \cdot 4 cdot 2 ] . #
# \qquad \qquad \qquad \qquad \qquad = \ ( 2 x - 5 )^3 ( x^2 + x + 1 )^4 [ 5 ( 2 x - 5 ) ( 2 x + 1 ) #
# \qquad \qquad \qquad \qquad \qquad \qquad \qquad + 8 ( x^2 + x + 1 ) ] #
# \ = \ ( 2 x - 5 )^3 ( x^2 + x + 1 )^4 [ 5 ( 4 x^2 - 8 x - 5 ) + 8 x^2 +8 x + 8 ] #
# \ = \ ( 2 x - 5 )^3 ( x^2 + x + 1 )^4 [ 20 x^2 - 40 x - 25 + 8 x^2 +8 x + 8 ] #
# \ = \ ( 2 x - 5 )^3 ( x^2 + x + 1 )^4 ( 28 x^2 - 32 x - 17 ); #
# "which is as your example, as given, ended." #
# "I hope this helps !!" #