Question

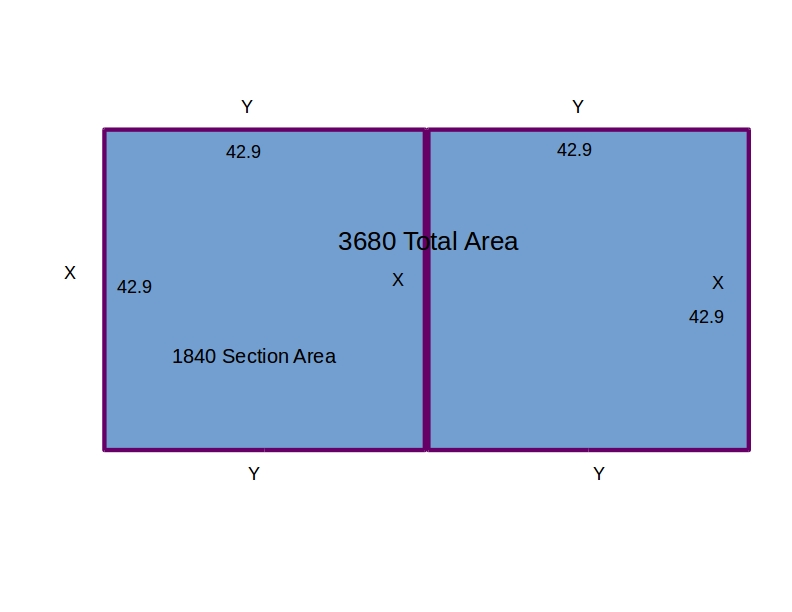
Find the dimensions of the rectangular corral split into `2` pens of the same size producing the greatest possible enclosed area given `300` feet of fencing?

Answer 1

Total rectangle = `42.9 xx 85.8`
Area = `3680`

Explanation:

First, the "maximum" area is irrelevant - it can only be the product of the sides, which is the same for any rectangular perimeter.

In this case it is really just two identical rectangles with a shared side. SO, if we call them "X x Y" rectangles, the overall fence used is `3X + 4Y = 300`. The area of the combined space is `X xx 2Y`, which is the same area for any constant sum of X and Y.

Because the relative values do not affect the area, we can take a square as a reasonable geometry for the individual sections. In that case, `X = Y`, so the overall fence use is `3X + 4X = 300`
`X = 300/7 = 42.9 = Y`
The total area is `X xx 2Y = 42.9 xx 42.9 xx 2 = 3680`