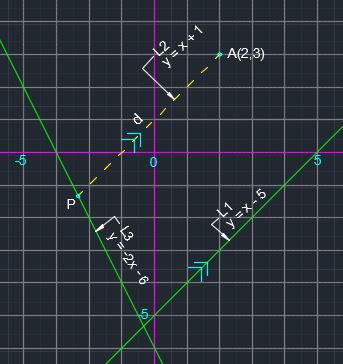
Let equation of #L1# be #y=x-5# , which has a slope #m# of #1#.
and equation of #color(red)(L3)# be #color(red)(y=-2x-6)#
Draw a line from #A(2,3)#, parallel to #L1#, to meet #L3# at #P#, as shown in the figure.
#AP# is the distance measured parallel to #L1# from #L3#
Let the line joining #A# and #P# be #L2#.
Given that #L2# is parallel to #L1#,
#=> L2# has the same slope #(m=1)# as that of #L1#,
Now find the equation of #L2# through #A(2,3)# with a slope of #m=1#.
#y=mx+b#
#=> 3=1xx2+b, => b=1#
#=># equation of #color(red)(L2)# in slope-intercept form is #color(red)(y=x+1)#
Set the equations of #L2 and L3# equal to each other to find the intersection point #P#
#=> x+1=-2x-6, => x=-7/3#
#=> y=-(7/3)+1=-4/3#
#=># coordinates of #P = (-7/3,-4/3)#
The distance from #A(2,3)# to #P(-7/3,-4/3)# is
#d=sqrt((-7/3-2)^2+(-4/3-3)^2)#
#=sqrt(338/9)~~6.13# units
