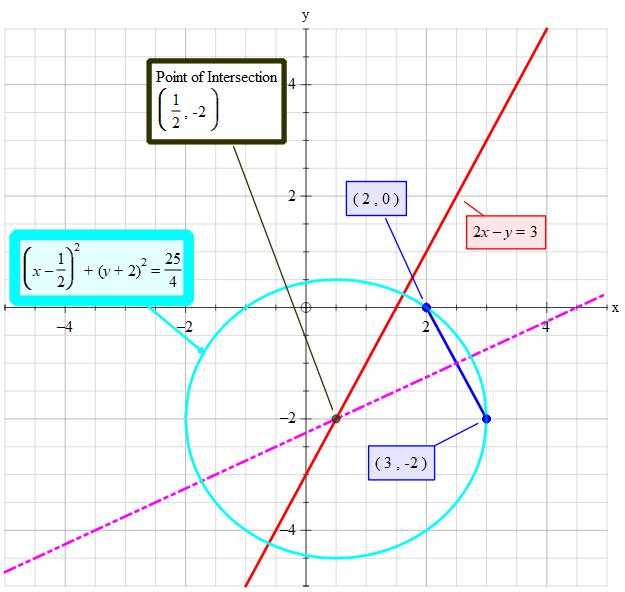
Lets have a look at what we have got.
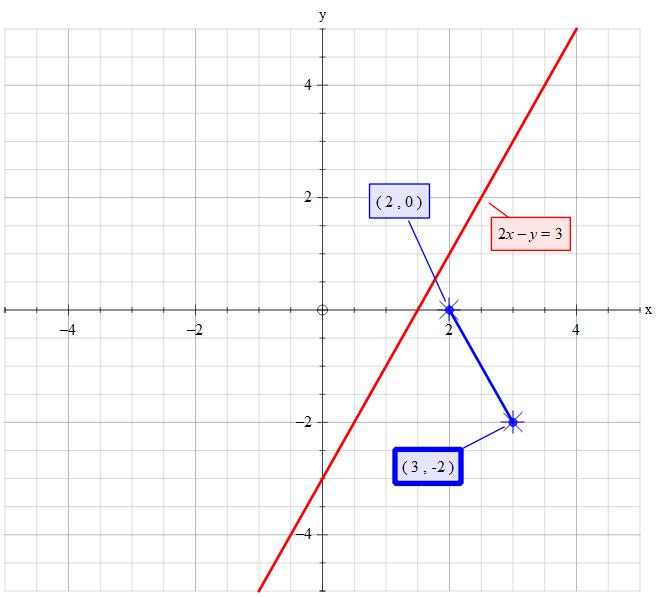
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Plan")#
#color(brown)("Step 1")#
Determine the equation of the line connecting the two points.
#color(brown)("Step 2")#
Determine the centre point between (3,-2) and (2,0)
#color(brown)("Step 3")#
Determine the equation if the line perpendicular to that between the two points and passing through the centre point.
#color(brown)("Step 4")#
Determine the point of intersection with #2x-y=3#
#color(brown)("Step 5")#
Determine the equation of the circle.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Doing the calculation")#
#color(brown)("Step 1 - Equation of line between the 2 points")#
Let #m# be the gradient
#m=(y_2-y_1)/(x_2-x_1)->(-2-0)/(3-2) = -2/1=-2#
#-2=(y-0)/(x-2) -> -2(x-2)=y#
#color(green)(y=-2x+4 color(red)(" Actually we only need the gradient "m#
......................................................................
#color(brown)("Step 2 - Mid point between the two coordinates")#
The mid point is the mean values
Set the mid point for #x# as #P_(1x)=(2+3)/2=5/2#
Set the mid point for #y# as #P(1y)=(0+(-2))/2=-1#
Set the mid point for #x and y# as #color(green)(P_1->(x,y)=(5/2,-1))#
......................................................................
#color(brown)("Step 3 - Equation of the perpendicular line")#
Gradient between the two given point is #m=-2#
The perpendiculat line will have the gradient #(-1)xx1/m = 1/2#
Thus relating this to the centre point we have
#m=(y-y_c)/(x-x_c) color(white)("dddd")->color(white)("dddd") 1/2=(y-(-1))/(x-5/2)#
#color(white)("dddddddddddddd")->color(white)("dddd")1/2x-5/4=y+1#
#color(green)(color(white)("dddddddddddddd")->color(white)("dddd")y=1/2x-9/4)#
We now have our two equation for the centre of the circle
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Step 4 - Determine the centre of the circle.")#
Note that #2x-y=3 -> y=2x-3#
#y=2x-3" "....................Equation(1)#
#y=1/2x-9/4" ".................Equation(2)#
#4Eqn(2)-Eqn(1)#
#3y=-6 => y=-2#
Substitute #y=-2# in #Eqn(1)#
#2x=1 => x=1/2#
#color(green)("Centre of the circle "->P_c->(x,y)=(1/2,-2))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Step 5")#
#color(brown)("The distance from the centre to point (2,0) -> radius")#
#r=sqrt( (x_("difference"))color(white)()^2+(y_("difference"))color(white)()^2)#
#r=sqrt((2-1/2)^2+(0-(-2))^2)#
#r=sqrt(9/4+4)#
#color(green)(r^2=25/4)#
So the equation of the circle is #(x-1/2)^2+(y+2)^2=25/4#