(Sir, actually question is Find the distance of the centre of the circle x²+y²+z²+x-2y+2z=3,2x+y+2z=1 from the plane ax+by+cz=d where a,b,c,d are constant.Also find the equation of right circular cylinder whose base curve is the circle in above.Sir,I need help in solving the second part of this question. on Find the equation of right circular cylinder whose curve is the circle in #(x+1/2)^2+(y-1)^2+(z+1)^2=21/4# has as center the point #(-1/2,1,-1)#?)
·······························································································································
Giving the circle #C# defined by the intersection #S nn Pi# with
#S -> (x+1/2)^2+(y-1)^2+(z+1)^2 = 21/4# or
#S-> norm(p-p_0) = r_0#
with
#p = (x,y,z)#
#p_0 = (-1/2,1,-1)#
#r_0 = sqrt(21/4)#
and
#Pi-> 2x+2z-3=0# or
#Pi-> << p- p_1, vec n >> = 0#
where
#p_1 = (0,0,3/2)#
#vec n = (2,0,2)#
determine the right cylinder whose generating curve is #C = S nn Pi#.
The center of #C# is given by the projection of #p_0# onto #Pi# which is determined as the intersection #p_2 = L_1 nn Pi# where
#L_1->p_0+lambda vec n# and
#<< p_0+lambda vec n - p_1, vec n >> =0# solving for #lambda#
#lambda = - << p_0, vec n >>/norm(vec n)^2# and then
#p_2 = p_0-(<< p_0, vec n >>)/norm(vec n)^2 vec n = (1,1,1/2)#
now the #C# circle's center is at #p_2# with radius #r_c# determined as
#r_c^2 = norm(p_0-p_2) (r_0-norm(p_0-p_2))# giving
#r_c = 1/2sqrt(3(sqrt42-6))#
so the cylinder #Y# must be tangent to #S_2# with orientation given by #vec n# where
#S_2 -> norm(p-p_2) = r_c#
Assuming the generating line given by
#L_g ->p_g+mu vec n# we have
#norm(p_g+mu vec n-p_2)^2= r_c^2# or
#norm(p_g-p_2)^2+2 mu << p_g-p_2, vec n >> + mu^2 norm(vec n)^2= r_c^2#
solving for #mu#
#mu = (- << p_g-p_2, vec n >> pm sqrt(<< p_g-p_2, vec n >>^2-norm(vec n)^2(norm(p_g-p_2)^2-r_c^2)))/norm(vec n)^2#
but the generating line must be tangent to #S_2# then
#<< p_g-p_2, vec n >>^2-norm(vec n)^2(norm(p_g-p_2)^2-r_c^2)=0#
Now considering #p_g = p# and substituting we obtain the cylinder equation
#Y->6 sqrt[42] + 4 x - 4 x^2 + 16 y - 8 y^2 - 4 z + 8 x z - 4 z^2-45=0#
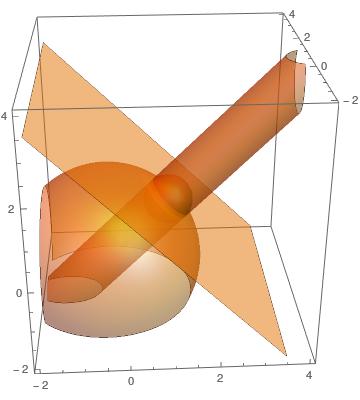
Attached a plot showing the arrangement.