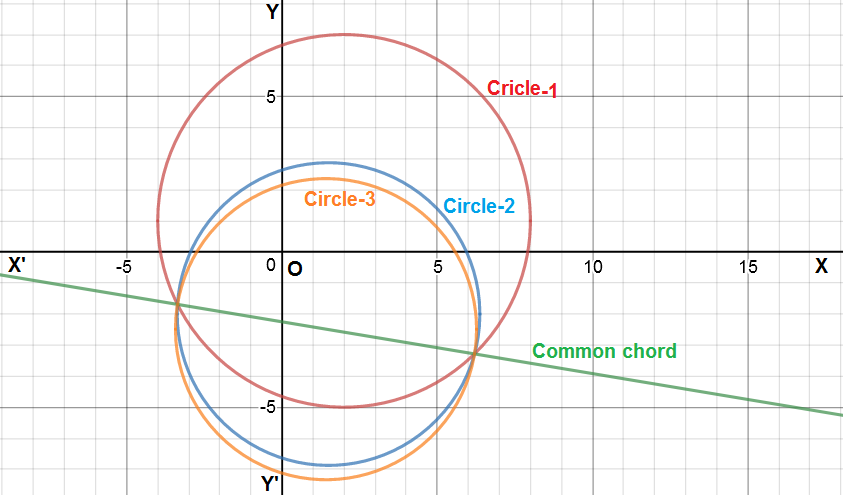
Equations of
#"Circle"_1->x^2+y^2-4x-2y-31=0.....[1]#
#"Circle"_2->2x^2+2y^2-6x+8y-35=0#
#=>"Circle"_2->x^2+y^2-3x+4y-35/2=0.....[2]#
Subtracting [1] from [2] we get the equation of common chord of the two given circles.
#x+6y+27/2=0......[3] #
Now equation of set of circles having common chord represented by equation [3] is given by
#"Circle"_1+lambda"Circle"_2=0#, where #lambda # is a parameter.
#=>x^2+y^2-4x-2y-31+lambda(x^2+y^2-3x+4y-35/2)=0#
#=>(1+lambda)x^2+(1+lambda)y^2-(4+3lambda)x-(2-4lambda)y-(31+35/2lambda)=0......[4]#
#=>x^2+y^2-(4+3lambda)/(1+lambda)x-(2-4lambda)/(1+lambda)y-(31+35/2lambda)/(1+lambda)=0#
Obviously the coordinates of the centers of the set of circles will be
given by #((4+3lambda)/(2(1+lambda)),(2-4lambda)/(2(1+lambda)))#
We are to find out the equation of that circle which will have the equation [3] as diameter, So the coordinates of the center should satisfy equation [3].
Hence
#(4+3lambda)/(2(1+lambda))+6xx(2-4lambda)/(2(1+lambda))+27/2=0 #
#=>4+3lambda+6xx(2-4lambda)+27/2xx2(1+lambda)=0 #
#=>4+3lambda+12-24lambda+27+27lambda=0 #
#=>43+6lambda=0 #
#=>lambda=-43/6#
Inserting the value of #lambda# in [4] we can get the required equation of the circle
#(1+lambda)x^2+(1+lambda)y^2-(4+3lambda)x-(2-4lambda)y-(31+35/2lambda)=0#
#=>(1-43/6)x^2+(1-43/6)y^2-(4+3(-43/6))x-(2-4(-43/6))y-(31+35/2(-43/6))=0#
#=>-37/6x^2-37/6y^2+35/2x-92/3y+1133/12=0#
#=>74x^2+74y^2-210x+368y-1133=0....[5]# #[color(orange)("Circle"_3)]#


