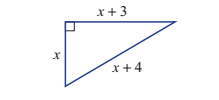
Find the exact perimeter of this triangle?

enter image source here

Answer is: #6sqrt2# #+ 10# units

1 Answer
Jim G.
Jul 12, 2017

#"see explanation"#

Explanation:

#"to find the value of x use "color(blue)"Pythagoras' theorem"#

#"that is"# the square on the hypotenuse of a right triangle is equal to the sum of squares on the other two sides.

#rArrx^2+(x+3)^2=(x+4)^2#

#"expand brackets using the FOIL method gives"#

#x^2+x^2+6x+9=x^2+8x+16#

#"collect terms on left side and equate to zero"#

#x^2-2x-7=0larra=1,b=-2,c=-7#

#"solve using the "color(blue)"quadratic formula"#

#x=(2+-sqrt(4+28))/2=(2+-sqrt32)/2#

#color(white)(x)=(2+4sqrt2)/2=1+2sqrt2larr" positive only"#

#"perimeter "= x+x+3+x+4=3x+7#

#color(white)(perimeter)=3(1+2sqrt2)+7#

#color(white)(perimeter)=3+6sqrt2+7#

#color(white)(perimeter)=6sqrt2+10larr" exact value"#

Related questions
Impact of this question
5002 views around the world
You can reuse this answer
Creative Commons License