This problem is solved using the Pythagorean Theorem and knowledge of "soh-cah-toa".
Recall that "soh-cah-toa" reminds us that #sin(x) = "opposite"/"hypotenuse"#, #cos(x) = "adjacent"/"hypotenuse"# and #tan(x) = "opposite"/"adjacent"#, where 'opposite', 'adjacent' and 'hypotenuse' refer to sides of a right triangle.
Our equality #tan(x) = 5# refers to a right triangle where the side opposite from angle #x# is 5 times larger than the side adjacent to #x#. The following is one such triangle (not drawn to scale).
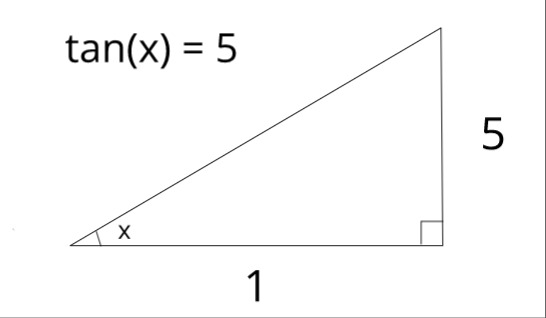
Using the Pythagorean Theorem, we can find the length of the hypotenuse.
#a^2 + b^2 = c^2#,
#1^2 + 5^2 = c^2#,
#26 = c^2#,
#c = sqrt(26)#.
Then #cos(x)# refers to our same triangle. See that #cos(x) = "adjacent"/"hypotenuse" = 1 / sqrt(26)#.
Note: This triangle extends up and to the right, into the first quadrant.


