Find the exact value of: csc^2(17pi/4) How do I do problems with the sin, cos, tan...etc raised to the power of 2?
2 Answers
Mar 20, 2015
I would try to simplify your angle.
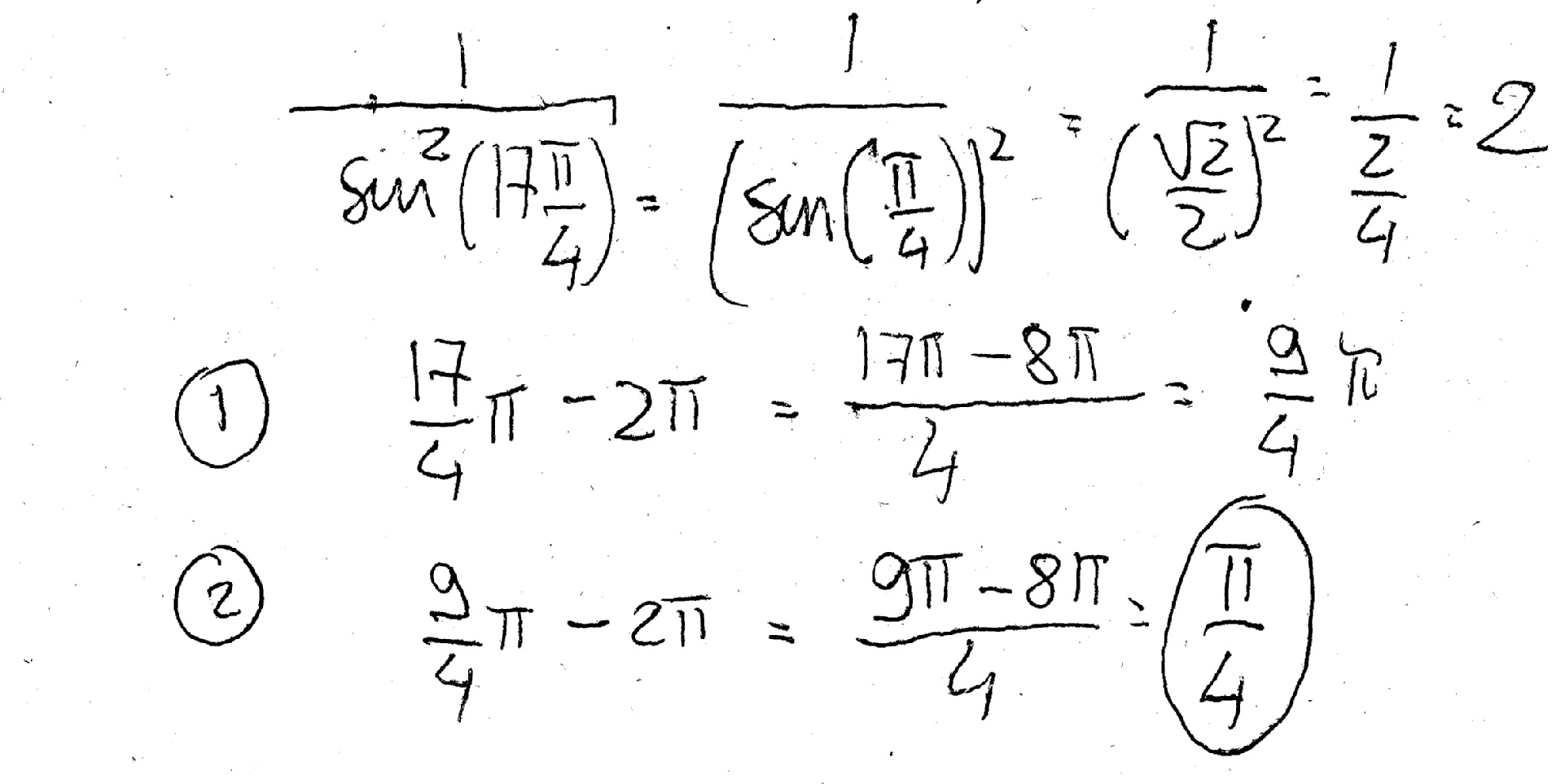
Mar 20, 2015
Keep in mind that when we write a trig function to a (positive) power, we mean evaluate the trig function, then raise the value to the power.
So, to find
That is: find
Note:
This convention does not include
We use the
Example:
So,


