Find the exact value of tan(\theta) if csc(\theta)=-4/3 and the terminal side of the \theta lies in the third quadrant?
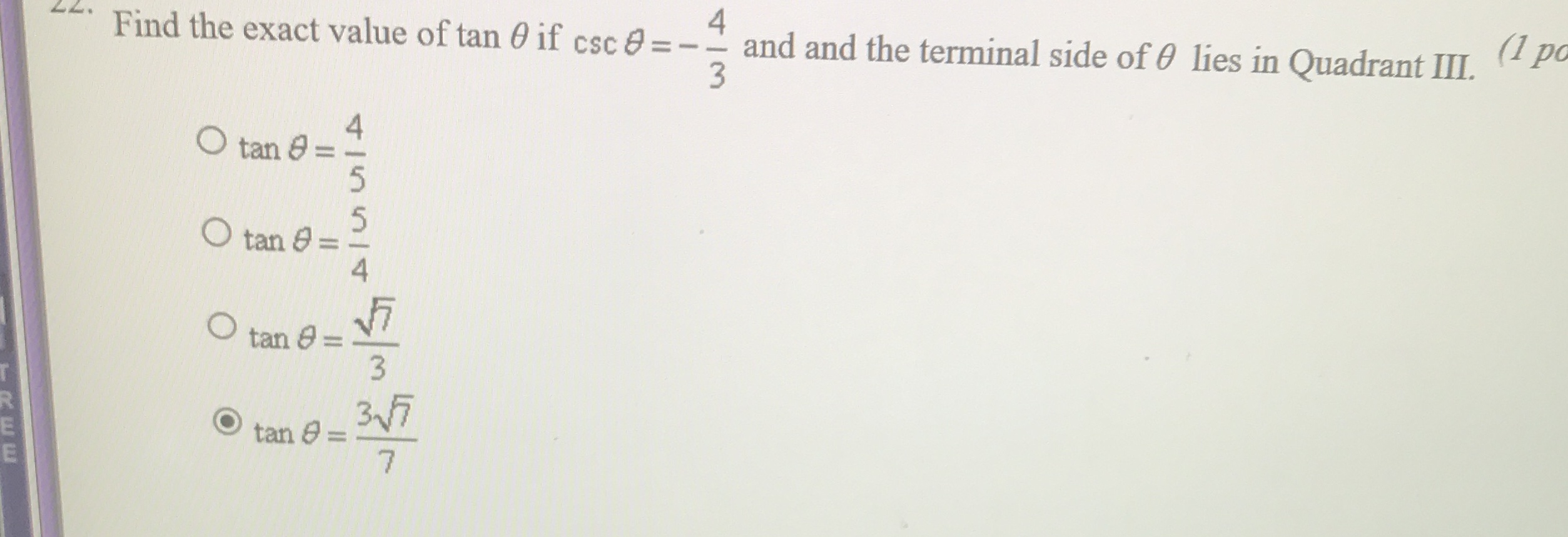
2 Answers
You marked the correct answer;
Explanation:
Using the reciprocal identity
we can rewrite the given statement:
This means that the ratio of the opposite side to the hypotenuse is
Since this is in the third quadrant, this value must be negative, so
Now, since we know that
Explanation:
"using the "color(blue)"trigonometric identities"
•color(white)(x)sintheta=1/csctheta" and "tantheta=sintheta/costheta
•color(white)(x)sin^2theta+cos^2theta=1
rArrcostheta=+-sqrt(1-sin^2theta)
csctheta=-4/3rArrsintheta=-3/4
theta" is in third quadrant where "costheta<0
rArrcostheta=-sqrt(1-(-3/4)^2)
color(white)(rArrcostheta)=-sqrt(7/16)=-sqrt7/4
rArrtantheta=-3/4xx-4/sqrt7=3/sqrt7=(3sqrt7)/7

