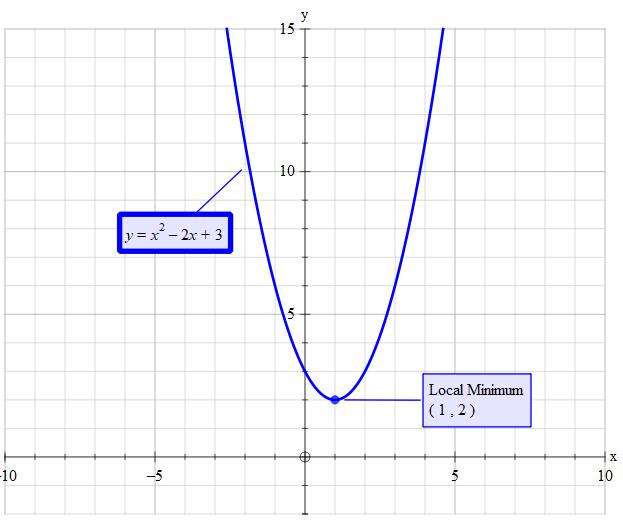
Find the extreme values of #y= x^2 − 2x + 3#?
3 Answers
Minimum at
Explanation:
To get the minimum set the derivative
equal to zero:
which solves for
Since the highest exponent in this equation is 1 it only has one solution.
By doing the second derivative
The maximums are, since the highest exponent in the original equation (2) is even and has a positive factor, at
Solution part 1 of 2: All answer for
Upper bound
Explanation:
The term
So to use a none mathematical term;
So
Tends to
Note that if
Also that if
Thus we write:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Foot note
As the
Solution part 2 of 2: The whole and final answer.
Explanation:
Given:
As the
To determine this we need the vertex (bottom of the
This will be
Looking at the given equation notice that
But
Given
Substitute
Vertex