Find the integral ?
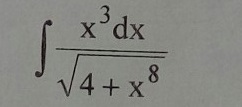
2 Answers
Jun 27, 2018
Explanation:
=
After using
this integral became
=
=1/4*u+C#
After using
Jun 27, 2018
Explanation:
Here,
Subst.
So,


