Question

Find the number a such that the line x = a divides the region bounded by the curves y = x, y = 0, and x = 4 into two regions with equal area. Give your answer correct to 3 decimal places?

Answer 1

`a = 2sqrt2` So `a ~~ 2.828`

Explanation:

Here is a picture of the two regions:

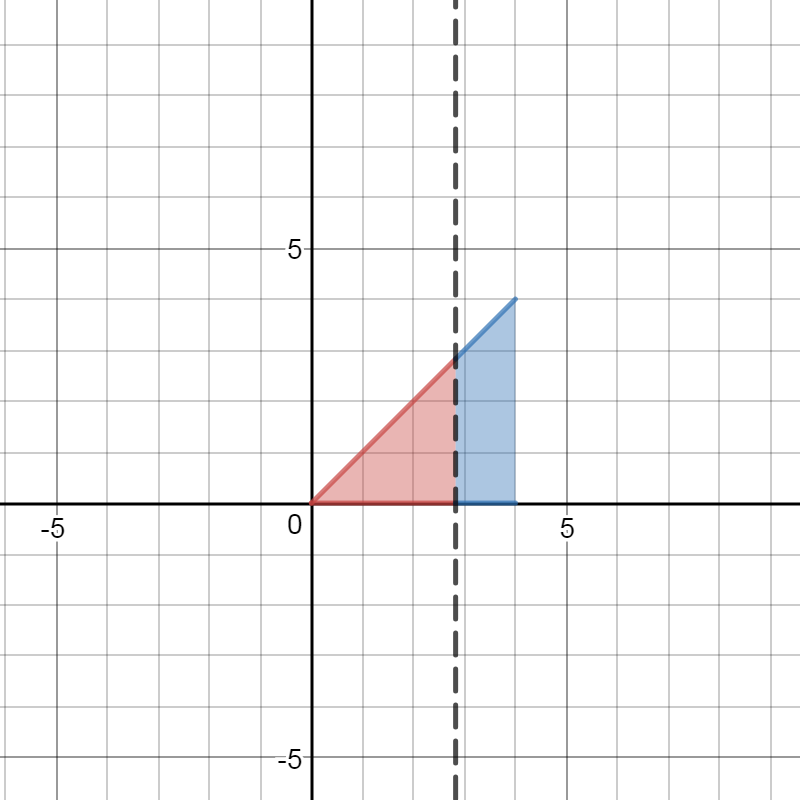
The area of the triangle is `1/2 a^2`

The blue ares is a rectangle with a triangle on top. Its area is `a(4-a)+1/2(4-a)^2`

Set the areas equal to each other and solve.

`1/2 a^2 = a(4-a)+1/2(4-a)^2`

`a^2 = 8a-2a^2+a^2-8a+16`

`2a^2 -16 = 0`

`a = sqrt8 = 2sqrt2`

Answer 2

`color(red)(a=2sqrt2)`

Explanation:

.

Let's start out with a figure where the given functions are graphed:

`y=x` is drawn in dark purple.

`y=0` is the `x`=axis in black.

`x=4` is the vertical line in red.

`x=a` is the vertical line in green.

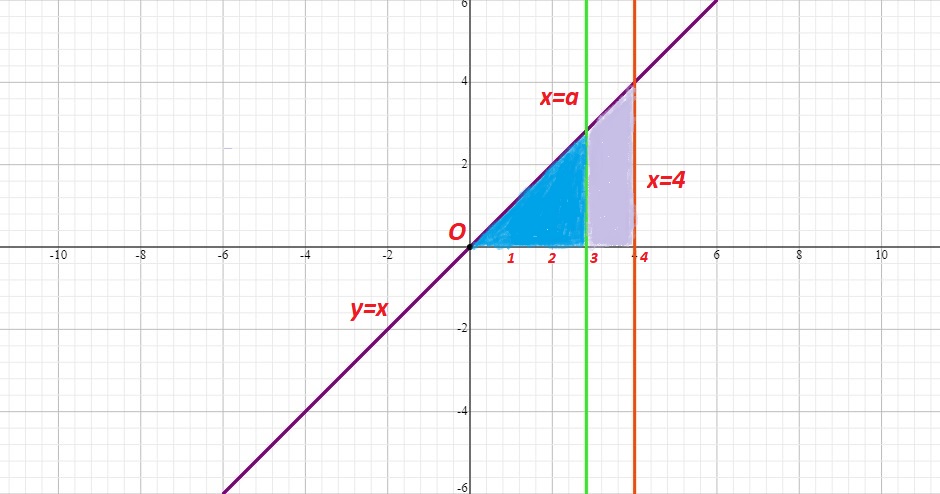
The region bounded by `y=x`, `y=0`, and `x=4` is the area comprised of the blue-shaded and lavender-shaded sections together.

Line `x=a` divides the bounded region into two parts as shown. We need to find `a` such that this green line divided the bounded region in such a way that the blue area and the lavender area are equal.

We will calculate the area of the total bounded region using an integral. The integral of the function `y=x` evaluated between `x` values of `0` and `4` will give us that area:

`int_0^4xdx=(1/2x^2)_0^4=1/2(4)^2-1/2(0)^2=16/2-0=8`

The blue area can be calculated by taking the integral of the purple line and evaluating it between `0` and `a`:

`int_0^axdx=(1/2x^2)_0^a=1/2(a)^2-1/2(0)^2=a^2/2-0=a^2/2`

Since the blue area is supposed to be `1/2` the total bounded region:

`a^2/2=1/2(8)`

`a^2/2=4`

`a^2=8`

`color(red)(a=2sqrt2)`